Incorporation of adjustments to the levelised cost for degradation are addressed on this page. A lot of assets degrade in different ways as do humans. In some cases like solar and batteries, the entire plant degrades and you can adjust the recovery of the total capital cost. In other cases such as for hydrogen, the degradation applies only to one cost item — the purchase of electricity. On this page I show you how to apply both types of degradation. I emphasize again that the you should worry much more about getting the levelised cost number right and less about your financial model which just proves that the levelised cost numbers are correct. The effects of degradation on levelised cost can include degradation only in input or fuel expense. The LCOE calculator attached to the button below can be used to evaluate degradation in the entire project or only the operating expense. Formulas and technical details are explained below.
.
.
Summary of Degradation Formulas
.
There is degradation of the total output which requires a kind of reverse inflation. The degradation calculations can be painful because they are different if you are using real or nominal LCOE and they require adjustments to both the capital charge portion of the LCOE and the operation and maintenance part of the LCOE formula. In general you can think of degradation as the opposite of inflation where things are getting smaller instead of getting larger. Here is the step by step approach. Note that there are different degradation calculations for nominal LCOE and Real LCOE. When you make adjustments to the rates for PMT and for PV calculations, you should be careful with the denominator. Note that the tax adjustment — divided by (1-t) is made to the PMT function using the nominal IRR adjusted for degradation.
.
Part 1: Adjustments to Real LCOE for Overall Output Degradation.
Step 1: Compute Real Rate as (1-Nominal Rate)/(1+Inflation Rate) – 1
Step 2: Compute Real Rate with overall degradation effect:
Real rate with degradation = (1+real rate)/(1-degradation) – 1
This adjusted rate is applied to the PMT function and to the O&M function for overall degradation.
Step 3: Factor for O&M to increase O&M (Real rate with adjustment is higher):
Factor for Real O&M = PV(Real Rate Adjusted, Life,-1)/PV(Real Rate,Life,-1)
Real O&M = Initial Real O&M x Factor
.
Part 2: Adjustments to Nominal LCOE for Overall Output Degradation as with Solar Project
Lets start with the case of computing the carrying charge for the case where nominal levelized cost is computed. In this case the PMT formula should be adjusted in a similar manner as it is in the real case for inflation. Remember that you can conisder degradation as negative inflation. If degradation occurs, then you must recover more money in nominal terms the account for the reduction in output over time.
This is a bit more confusing. The O&M goes up because it should inflate and it goes up further because of degradation. So there are two adjustments to the O&M for nominal levelization. You compute a PV factor adjustment and use the real rate in the numerator and the nominal rate adjusted for degradation in the denominator. To begin the discussion, recall the inflation rate adjustment for O&M in the nominal case.
On another page I have explained how to make adjustments for inflation in operation and maintenance when computing the levelized cost on a nominal basis. The adjustment is necessary because the reported operating and maintenance is generally stated in current dollars or euros etc. — on a real basis. If you are computing the nominal LCOE and you have the real O&M expense, then you can increase the O&M Expense using the PV (not the NPV) formula in excel. You can think about the basic fact that if you use the PV formula with the life of the project, then the PV gives you a higher number when you have a lower discount rate.
Step 1: Compute the adjusted nominal IRR for degradation as
Adjusted Nominal Rate = (1+Nominal Rate)/(1-Degradation Rate) – 1
Step 2: Apply the Adjusted Nominal Rate in the PMT function
Step 3: Adjust the Initial O&M.
You can use a factor as follows:
Nominal Case: Factor = PV(Real Rate, Life, -1)/PV(Nominal Rate, Life, -1)
This factor will be above 1.0 if the inflation rate is positive and the real rate is below the nominal rate.
Now to the degradation adjustment. To begin, you can compute the real O&M cost using the PV formula. You can do this in two steps.
Adjustment Factor1 = PV(Real Rate, life, O&M)/PV(Degradation Adjused Real Rate, Life, O&M).
Adjustment Factor2 = PV(Real Rate, life, Adjusted O&M)/PV(Nominal, Life, O&M).
O&M for Nominal = Current O&M x Adjustment Factor2
.

.
.
Inclusion of Degradation in the Levelised Cost using adjustments to both Carrying Charges and O&M Costs
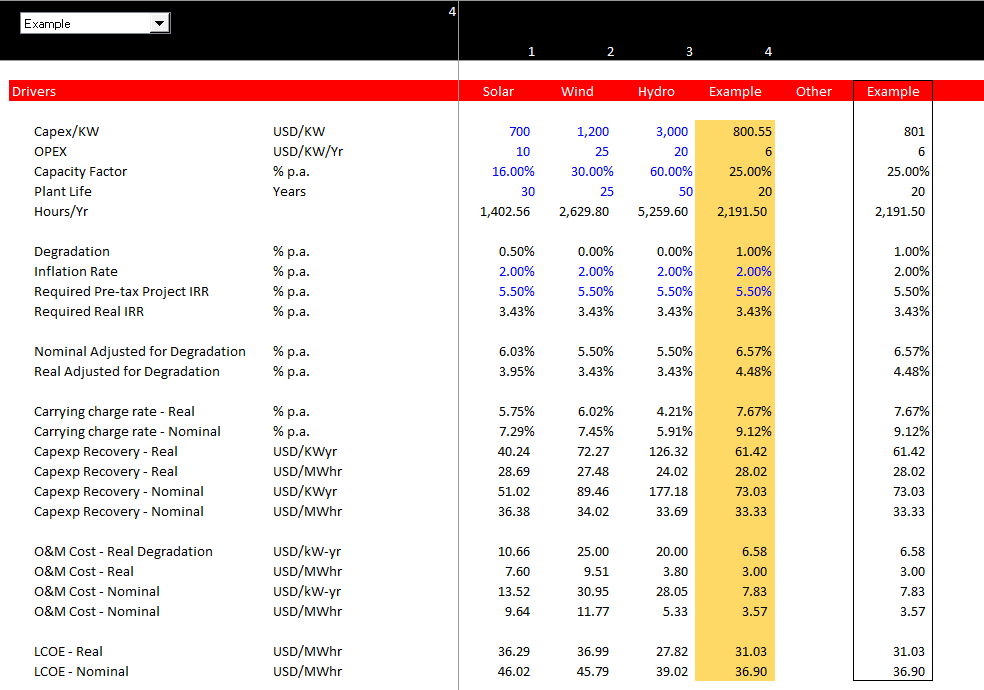
The formulas below evaluate levelised cost when the quantity of the units change. Different amount of units affects the weighting of the levelised price. For example, if the number of units is half of the units when the units start and if the price changes, then weighted average price changes. Without discounting, the screenshot below is 13.33. The price is not the average of 15.00 because you should give less weight to the price when there is less generation.
You should make changes to both nominal and real LCOE and you should make operating expense adjustments. The adjustments are represented by the following equations:
Adjusted Target IRR for Degradation = (1+Nominal IRR)/(1-Degradation)
Adjusted Real IRR for Degradation = (1+Real IRR)/(1-Degradation)
O&M Factor Nominal = PV(Real IRR,Life,-1)/PV(Adjusted Nominal IRR,life,-1)
O&M Factor Real = PV(Adjusted Real IRR,Life,-1)/PV(Real IRR,life,-1)
When you think about things, the levelised nominal cost is a silly number. Think about a hydro plant than may last 80 years. The nominal levelised cost is the flat value over 80 (with a minor adjustment for inflation in O&M expenses discussed below). With even a minor rate of inflation like 2%, the real value in 80 years is a very small percent of the value in the first year (divide by 1.02^80) — 4.9 times. It would be much better to compute the current value that, when inflated, gives you the target return. In simple terms this involves using a real cost of capital as described below.
Degradation with for a Single Expense Rather than the Entire Project (Hydrogen Case)
As stated above, for an electrolyzer the degradation can be for the quantity of electricity purchased rather than for the entire project.
PV(Real, Life,-1)/PV(Nominal,Life,-1)
Adusted Nominal = (1+Nominal)/(1-Real) – 1
Final Factor = PV(Real,Life,-1)/PV(Adusted Nominal,Life,-1)
.
