This page addresses the effect of taxes on the levelised cost of electricity. Addition of tax to the LCOE adds complexity and should be done to produce the actual cost that is reflected in financial models. The tax issues invlove using the formula 1/(1-t) to reflect the fact that taxes paid on equity increase the capacity charge component and this increases creates higher taxes. As with discussion of other issues you can use the after-tax LCOE, LCOH, LCOS or the levelised cost per unit of just about anything is to make an initial evaluation of the business case for different strategies. In using levelised cost per unit to evaluate business strategy, it is effective to first establish the costs of getting back your capital. This depends on the cost of capital, taxes, inflation, the life of the asset and the degradation rate in the productivity of an asset. This page works through how to compute the carrying charge components of the LCOE. With the carrying charge rate, you can put your own capital cost per kW, operating cost, capacity factor and derive the total LCOE. For example, if the renewable LCOE is less the cost marginal cost of energy, then consumer bills will be reduced from using more solar power. The LCOE in turn is driven by the carrying charge rate as these technologies are very capital intensive (much more capital intensive than a refinery).
In discussing the different techniques, I emphasize that the real cost without inflation rather than the nominal cost is the appropriate benchmark for comparing technologies that have different capital and operating costs. When you can measure the correct cost of something, it is a big deal. You can then evaluate business strategies that work with the most effective cost cases. For example, if you are evaluating hydrogen options, it may be better to put electrolyzers at the customer site (paying a higher price because of economies of scale), and oversize the electrolyzers so you only use solar power during sunny periods. The file that you can download by clicking the button below includes my LCOE calculator with some advanced issues related to taxes, financing, degradation, inflation and the lifetime of assets. The second file is the standard calculator without the ITC and the depreciation.
.
Excel File with Levelised Cost of Electricity Mechanics Including Detailed U.S. Tax Aspects and ITC
.
.
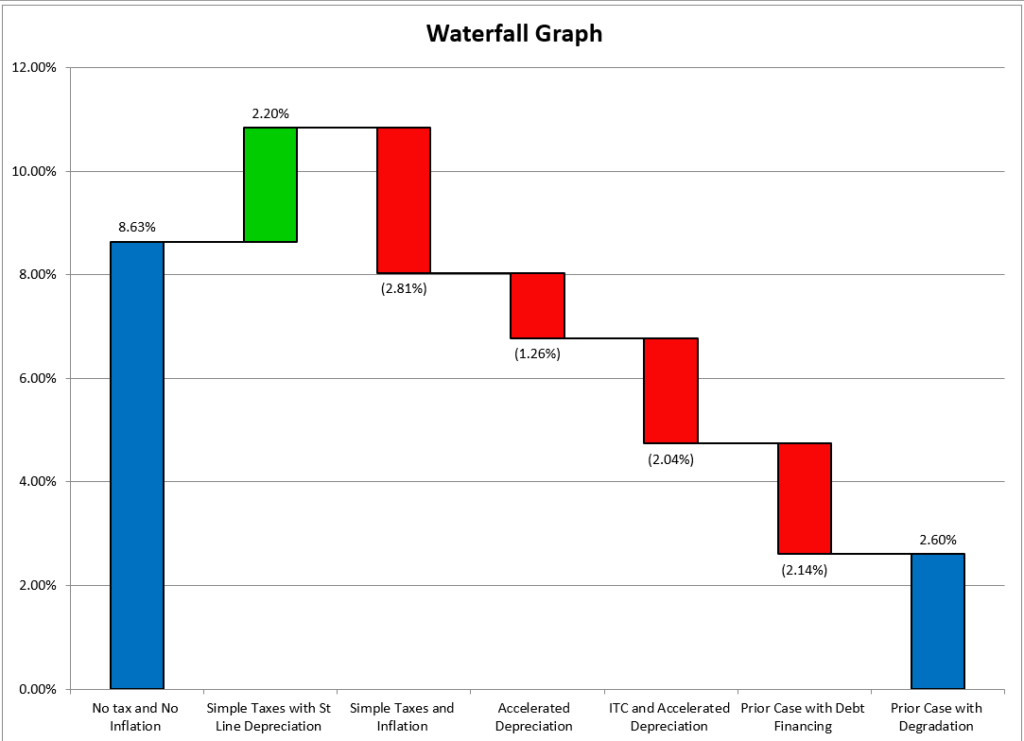
The carrying charge converts a one-time cost (sometimes referred to as overnight cost) into an annual cost. Carefully establishing carrying charge rates can make the analysis of different alternatives much more effective. The first part below walks through different components of the carrying charge that include evaluating project life, inflation, income taxes, investment tax credit, replacement capital costs, debt financing and maintaining a constant capital structure. On this page I explain how to adjust the carrying charge for taxes and tax depreciation. You can divide the process into two steps:
- The first step is dividing the PMT formula by (1-t) to account for taxes that will be paid on equity. The formula is PMT/(1-t)
- The second step is to compute the value of the tax shield as a percent from the PV of the tax depreciation at the pre-tax rate multiplied by the tax rate. The formula is PV(Nominal IRR, Life, -1/Life) x Tax Rate
.
.
.
Step 1: Using Pre-tax Capacity Cost by by (1-t)
.
If there was no depreciation, all of the required returns would increase by a factor of (1-tax rate) to recover taxes where you divided by (1-t). You cannot multiply the PMT formula by (1+t) because when you increase the PMT formula to recover taxes, this increases revenues and also increases taxes. This includes both the real and the nominal payment as follows:
Nominal Payment factor After tax = PMT/(1-tax rate)
Real Payment factor After tax = PMT/(1-tax rate)
.
Step 2: Computing the PV of the Tax Shield and Subtracting the PV of the Tax Shield from the Capacity Payment
.
But this payment factor does not account for the benefit of the depreciation tax shield. To account for the benefit of the tax shield you should compute the PV of the depreciation at the nominal and not the real discount rate. Here is the process:
- Compute the depreciation rate (this could be MACRS as in the Lazard model)
- Compute the PV of the depreciaiton rate at the nominal discount rate
- Start discounting in the first year of operation, not the first year of the construciton
- Mutiply the PV of the depreciation rate by the tax rate and divide by 1-t
- Use the PMT formula to compute the adjusted capacity charge
You should use the nominal discount rate rather than the real rate because the tax shield is the same in nominal terms no matter what happens to inflation. You can compute the PV of the tax shield in percentage terms using the depreciation rate. Then compute the NPV of the cost in nominal terms. Note that if the inflation rate and the nominal discount rate are higher, the value of the tax depreciation is less as it should be. Once you compute the PV, you can multiply the PV by the tax rate (if there were no taxes, the value of the tax shield would be zero.) So the value of the tax shield can be computed using the following formulas. When discounting, you use the pre-tax rate as the effects of gearing come into play when you apply the PMT to the net value.
PV of Depreciation = NPV (Nominal pre-tax WACC, Depreciation rate)
PV of SL Depreciation = PV (Pre-tax WACC, Tax Life, 1/Tax Life)
Tax Shield Value = PV of Depreciation * Tax Rate
CCR Adjusted for Tax = PMT x (1-Tax Shield Value)/(1-Tax Rate)
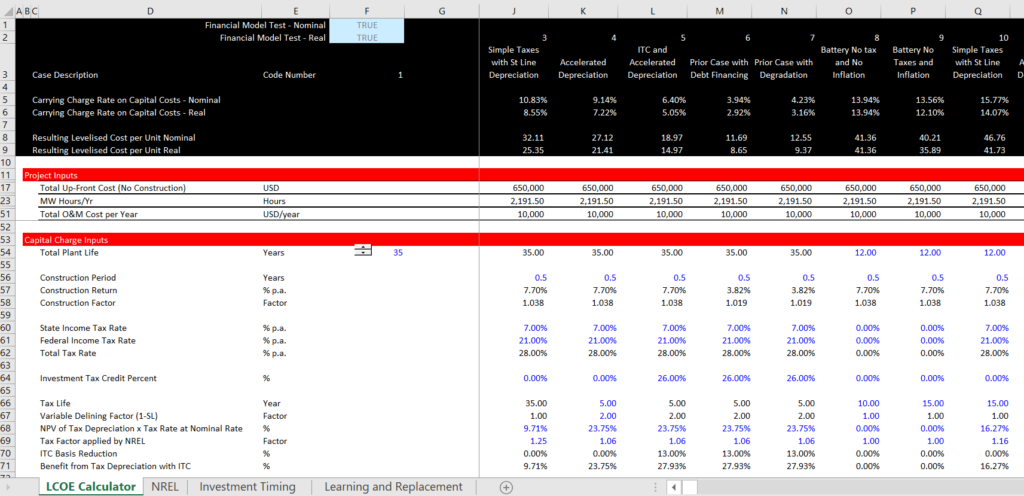
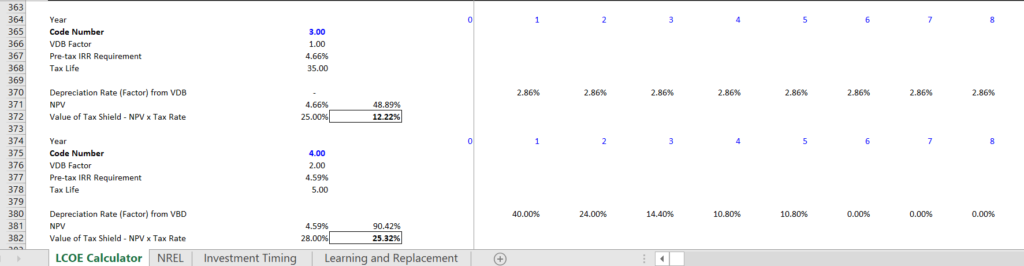
The last equation above for the CCR can be applied on either a real or a nominal basis. The next screenshots illustrate calculation of the tax shield. The first screenshot demonstrates that inputs that are required. The second screenshot demonstrates how the depreciation rate can be computed with the VDB formula and how the NPV is computed from the nominal WACC before accounting for the tax shield on the interest. The reason for using this pre-tax WACC is because the tax effects of interest are accounted for separately.
.
.
.
.
.
.
Investment Tax Credit and Government Grants
Case 4: Inclusion of Income Taxes and Tax Depreciation
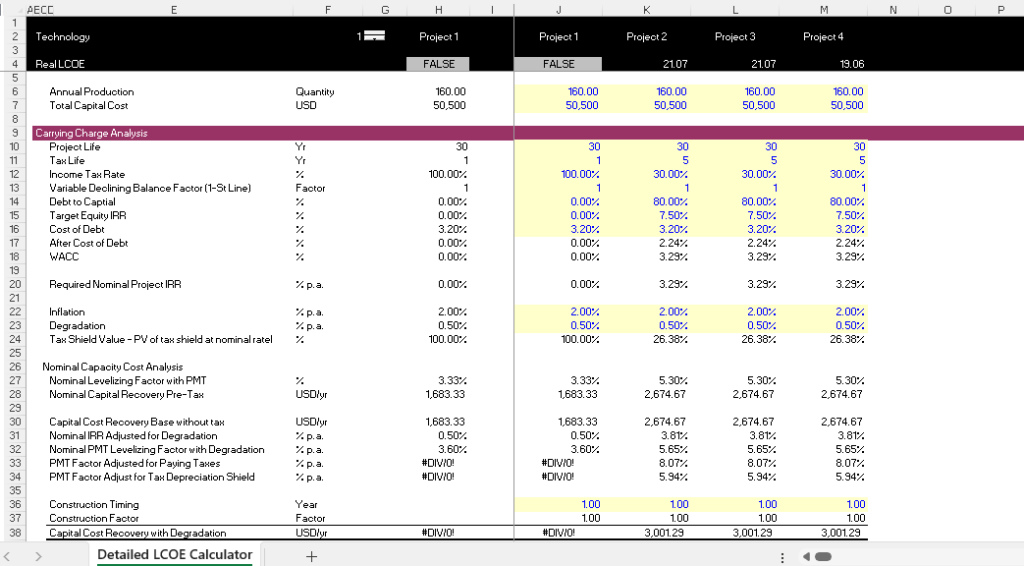
The next section evaluates levelised cost when the quantity of the units change. Different amount of units affects the weighting of the levelised price. For example, if the number of units is half of the units when the units start and if the price changes, then weighted average price changes. Without discounting, the screenshot below is 13.33.
.

.
Function tax_dep_shield(tax_life, fac, disc_rate, tax_rate)
Dim dep_rate(100) As Double
For yr = 1 To tax_life
If yr > 0 Then
dep_rate(yr) = WorksheetFunction.Vdb(1, 0, tax_life, yr - 1, yr, fac)‘ MsgBox ” Year ” & yr & ” dep rate ” & dep_rate(yr)
End IfNext yr
npv_of_dep = WorksheetFunction.NPV(disc_rate, dep_rate)
tax_dep_shield = npv_of_dep * tax_rate
End Function
.