This page illustrates how to compute taxes, cash flows and the balance sheet when taxes are computed in different currency than the primary currency of the model. I suggest carefully setting up an exchange rate at the top of the page and then compute the taxes (with NOL and FX adjustments) in the local currency. The first step is to compute EBITDA, depreciation expense, interest expense and other items that affect taxes in the local currency for taxes. When working with one trache of debt that is in a different currency than the model currency, you can again use the exchange rate at the top of the page to make conversions. In this case you can compute the effective interest rate or debt yield in the model currency and also the translation adjustment. Both adjustments are made using the percent change in the exchange rate. For example, if the debt is in a different currency (e.g. Euro or USD), then you can compute the FX loss (when the exchange rate increases) or the FX gain from the debt balance. You can compute the percent change in the exchange rate and multiply that percent by the opening balance of the debt (in Euro or USD) to compute the FX adjustment. With the FX adjustment, you can compute taxes in the local currency.
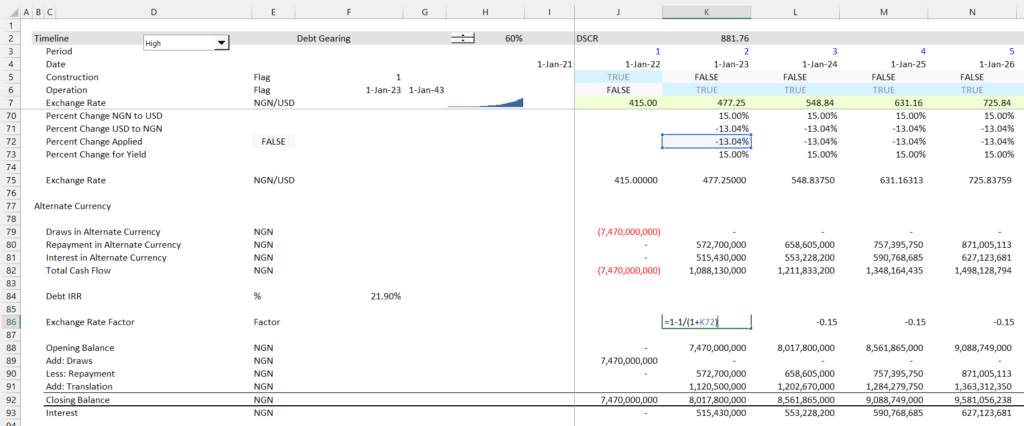
The step by step process for making a conversion from one currency to another is the following. In this example, I use a loan in USD which I call the base currency and then convert it to NGN — Niara which I call the alternate currency. The example would work just as well if the base currency was NGN and the alternate currency is USD. I show how to compute the translation adjustment and the interest rate in the alternate currency (in this case again the alternate currency is NGN.
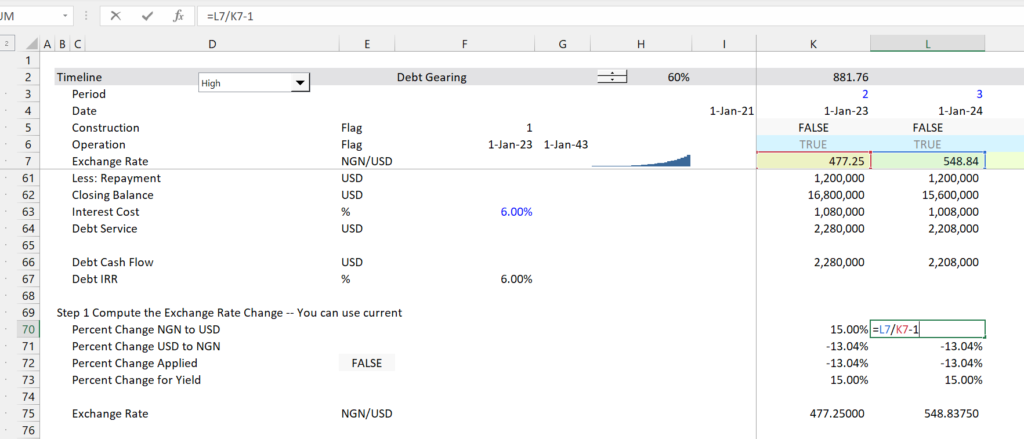
- Step 1: Compute the Exchange Rate using Alternate Currency/Base Currency (NGN/USD)
- Step 2: Compute the percent change in the exchange rate
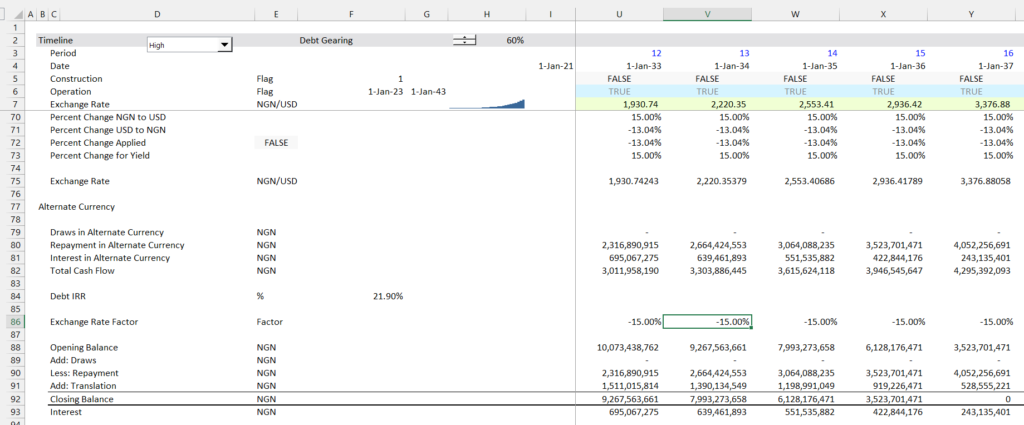
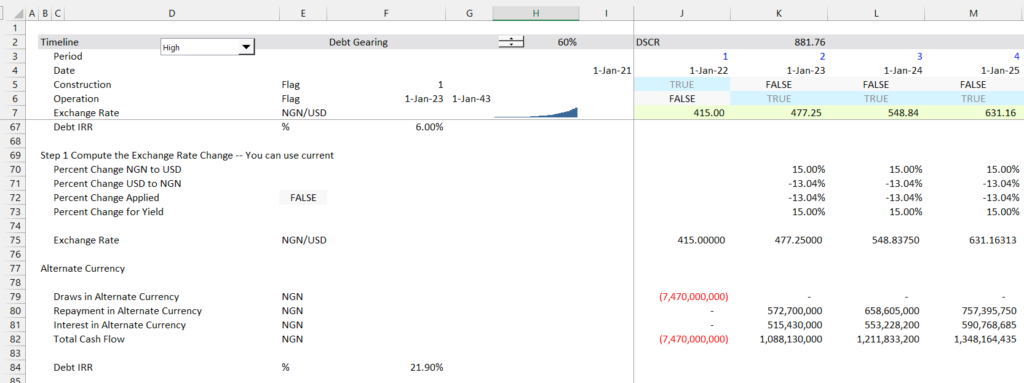
- Step 3: Translate cash flows at the exchange rate — draws, repayment and interest cost.
- Step 4: Compute the debt cash flow and the debt IRR
- Step 5: Compute the translation adjustment as opening balance multiplied by the percent change in the exchange rate
| Step 6: Compute the yield as (1+Base Rate) * (1+ Chg Rate) – 1 |
| Compute the yield as (Interest + Translation)/Open Balance |
Step 1 – Compute the Exchange Rate
The relationship between interest rates can be computed using the percent change in forward exchange rates. The forward exchange rate formula can be imagined for if a project or company wants to borrow in Euro rather than in USD to reduce interest costs. Currently, the interest rates in Euro are lower than the interest rates in USD and one might imagine borrowing in Euro to save money paid in interest and then signing an forward exchange rate contract to assure that there are not risk of losses from having to pay more USD back for the loan and lose the benefit of the lower interest rate. Assume a loan of 1 year and the steps to borrow in Euro would be the following:
- Borrow 100 US and convert this to Euro using an exchange rate of 1.1285
- This leaves you 88.61 Euro
- Pay interest on the loan in Euro. It is about -.5% right now
- The Interest you get back is .44 Euro or .50 USD
- Lock in the repayment of the USD in Euro the forward rate is 1.14 (you can get this from the internet
- Re-convert the Euro to USD in one year using the 1.14 exchange rate.
- This means you have to repay 101.02 USD
- At the end of the day you have borrowed 100 USD and you get back .5 and you pay 101.02
- The amount you get back is 100.52 which is a positive interest rate of .52% which is about the USD interest rate and you have gained nothing
This long and complex thing can be expressed in the more simple formula below:
Effective Interest Rate in USD = (1 + Euro Interest Rate)/(1 + Forward Exchange Change) – 1
Or, as the exchange rate change is 1.14/1.1285 = .9899
.52% = (1-.5%)/(.9899) = 1.005 and 1.005 – 1 = .5%
The process of computing taxes in the local currency and deriving the FX loss is illustrated in the file that you can download below and the associated video. A couple of files with examples of multiple currency are attached to the files below:
.
.
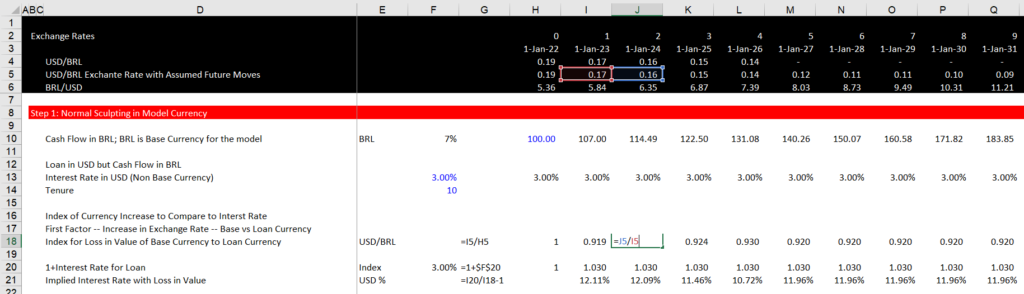
Step 1: Working with Forward Exchange Rates and Computing Implied Interest Rates
When working with multiple currencies, you can first put the currencies at the top of the sheet and evaluate the implied inflation rates. In the example below, we have gathered the forward exchange rate and then used the INTERPOLATE function. Note that the cash flow is stated in USD and the debt service is also in USD. But we assume that the loan is in EUR. In rows 17 to 19 we assume that the interest rate in EUR is 1.5% which you can use to compute the implied interest rate in USD. To do this you can:
- Compute the change in the exchange rate – could be devaluation or appreciation
- Add 1 to the loan interest rate in the alternative currency that is not the currency of the model
- The implied interest rate in the base currency is the 1+rate from step 2 divided by the devaluation or the appreciation.
.
.
.
.
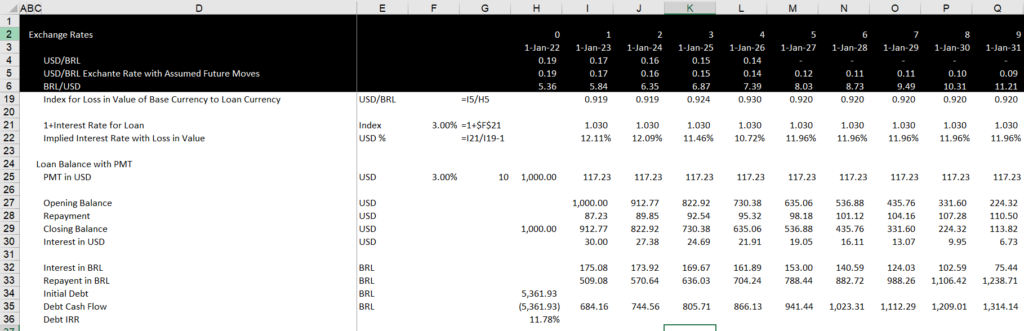
Step 2: Demonstration of IRR in Model Currency
Put the loan in both currencies with the translation adjustment. You can use the following steps:
- Compute a standard debt table/balance in the currency of the loan (for example in Euro if the model is in USD)
- Translate the repayment and the interest to the loan currency — these are the cash flows on the loan. For example if the loan is in Euro, compute the repayment and the interest in USD using the exchange rate at the top of the page)
- Compute the IRR on the cash flow of the loan in local currency — this should be something like the interest rates that you have computed above.
- Compute the yield on the loan in local currency. To do this you can use the formula:
Int Rate in USD = (1 + Euro Int Rate)/(1 + Forward Exchange Change) – 1
.
.
.
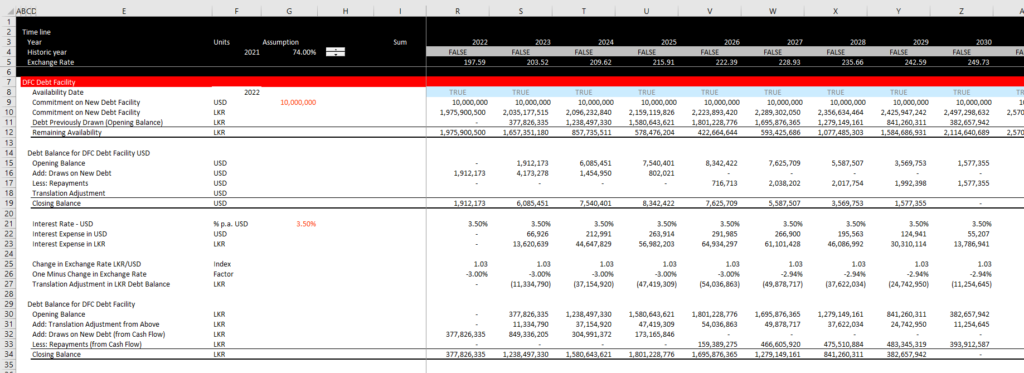
Step 3: Compute the Loan Balance with a Translation Adjustment to Verify the Interest Rate and the Translation Adjustment Method
If you are paying a loan with a lower interest rate than the interest rate of the model, then there will be a devaluation in the local rate. This means that you will have to pay more local currency
The increased local currency repayment will cause a loss on currency translation. Note that the if you convert the alternative currency to local currency when computing interest and repayment, there will be no cash flow affect of the currency adjustment. But when computing the loan balance, the translation should be included.
The translation adjustment should be computed using the opening balance of the loan and it should be compute using the percent change of exchange rate. In our example with Euro and USD, the USD/Euro rate would devalue or increase (for example the rate may move from 1.2 to 1.3). The percent change in the exchange rate is the new rate divided by the original rate. Compute the opening balance in the model currency and multiply that by the percent change in the exchange rate. When you make this adjustment, the closing balance measured in the model currency should end with a zero balance.
Translation adjustment = Percent Local/Alterantive Exchange Rate x Openinn balance
.
.
.
.
Step 2: Compute the Exchange Rate on the Opening Balance
Here, I am illustrating my method for evaluating a formula. You need to have the GENERIC MACROS file open and then you can press ALT, u.
.
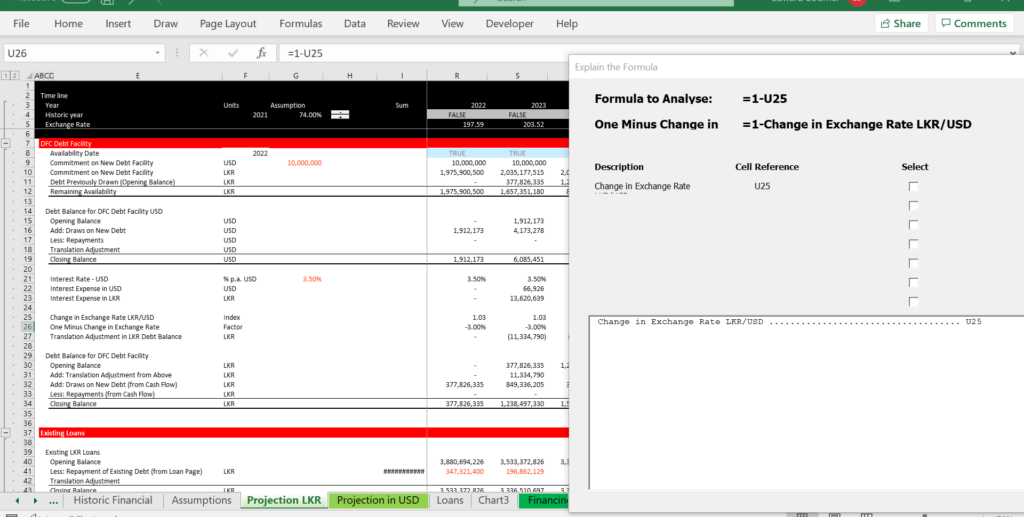
.
.
Once you compute the translation adjustment you can put it on the income statement. When you attach the cash flow to the profit and loss you can then convert the draws into the currency of the debt. This is illustrated in the example below. The file with the example is attached.
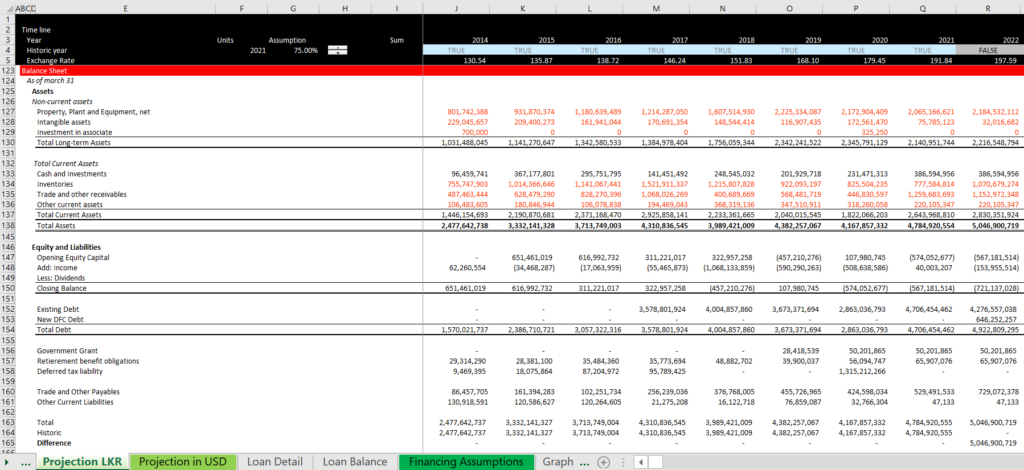
.
.
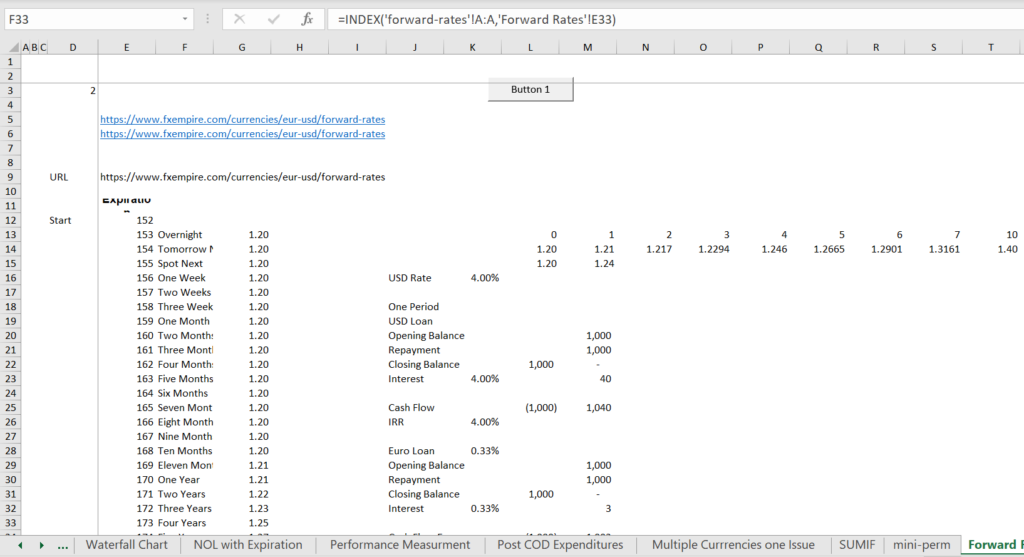
Finding Forward Rates
The screenshot below illustrates how you can find the forward rates which can then be used as the basis for computing the different interest rates and the different implied inflation rates derived from purchasing power parity.