Sometimes, the debt service is given by a fixed debt amount and a given debt service but you still want to maintain a given DSCR. When you use the sculpting mathematics using the formula Debt Service = CFADS/DSCR and Debt = NPV of Debt Servce, it is possible that negative repayments will occur.In this case you could think about a few things to do. First, you could change the price so that it moves around and produces the desired DSCR. Second, you could establish a cash reserve something like a maintenance reserve account and then pull money out of the reserve account when you need it to meet the DSCR requirement. Third, you could set up a revolving loan where you could borrow money when you need it and then pay it back when you have sufficient cash flow. In this page I illustrate how to work through these three options and evaluate the IRR result.
The situation of negative repayment is particularly true when either the cash flow pattern has a fast rate of increase or when there is a lot of volatility in cash flow from for example, battery replacements every three years or from low solar periods relative to high solar periods. As repayment = debt service – interest, the repayment can be negative when the required debt service from the CFADS/DSCR formula results in a lower value than the interest. When this occurs the bank may be reluctant to allow a negative repayment or what may be called a non-amortizing loan or a capitalizing loan. This page describes a few ways that you may address the problem. These methods include:
- Allow Negative Repayment
- Limit the size of the debt
- Create a cash reserve account
- Limit the debt service to the interest expense
- Add a working capital facility
Other than the first two methods, all of the techniques have an effect on the cash flow and can create a circular reference. The model examples on this sheet will walk through the different alternatives in the context of sculpting with multiple debt issues and either battery replacement or high seasonality.
.
I suggest thinking about the following step by step process.
- 1. Compute sculpting with the negative repayment that results from very low CFADS
- 2. With the negative payment, derive the amount of CFADS necessary to get to the DSCR with no repayment. Do this by computing Negative Repayment/DSCR
- 3. As many put things like working capital facilities and MRA changes into CFADS, do the same thing with amounts from step 2.
- 4. The amounts in step 2 can be modelled as revolver draws or withdrawals to something analogous to an MRA account.
- 5. With either modelling the negative repayments/DSCR as a revolver or an MRA account, you need to fund the MRA or repay the revolver (plus interest)
- 6. I suggest something like a cash sweep for both of these (MRA or revolver) where dividends are impacted.
.
Method 1: Allow Negative Repayment
In the first example, I illustrate a couple of examples that lead to negative repayments. The first is a seasonal case that is extreme for a solar project. The second is a case where expenditures are made every three years. The graphs in the screenshots below illustrate the cases with the negative repayments. In modelling the expenditures that can come in different time periods and arise in different amounts, you can use the XLOOKUP function. The XLOOKUP function with two zeros is like using the MATCH with an exact match. The sceenshots below illustrates the use of the XLOOKUP in setting up the model. The first sceenshot illustrates how the model accepts different timing and amount of expenditures.
.
.
.
.
Excel File with Fixed Debt Repayment and Mismatch of Cash Flow and Debt Service with Graphs
.
.
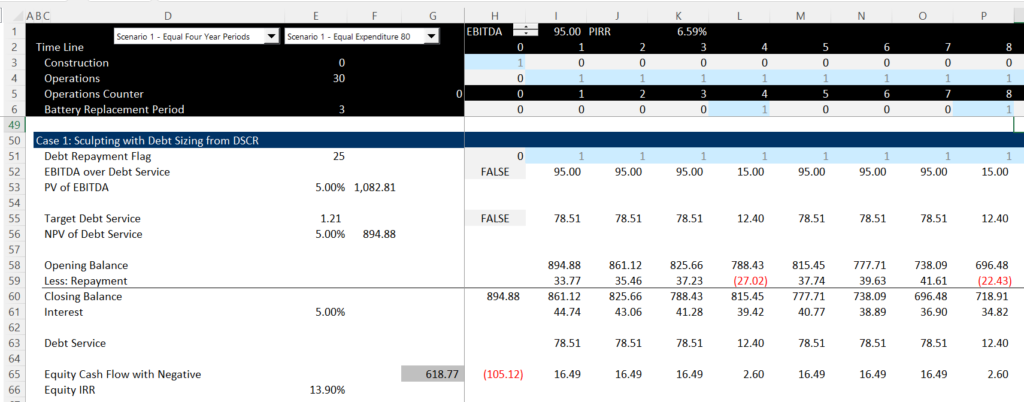
The next screenshot illustrates how sculpting is computed with negative sculpting when a capital expenditure like battery expenditures occur. Note the negative repayment that comes from the sculpting formula.
.
.
The negative repayment is the basis of the remainder of the discussion for the different methods below. The equity IRR in the graphs above is the basis for comparison of the different methods.
.
Method 2: Reduce the Debt Size
The first method is the worst method from the standpoint of the equity IRR. In this case, you can add a constraint in addition to the NPV formula that produces the total amount of the debt. This can be done using the following equations. In periods when there is negative cash flow, the DSCR is increased and the debt is reduced.
.
.
The same graphs shown above for the case where the debt size is reduced are showbelow. The graphs shown below illustrate that the equity IRR is reduced a lot.
.
.
Method 3: Implement a Reserve Account
The third method involves looking ahead and finding cash that can be used in a reserve account to deposit into the reserve account. The amount deposited in the reserve account is treated as a reduction in CFADS. For periods in which the reserve is used, the CFADS is increased. The trick is to find the available cash and then work backwards. The formulas and an illustration is shown below.
This is a horrible method the kills the IRR. You can compute debt service first as normal. Then you can compute the repayment and put in a flag for when the repayment is negative. You can compute the debt service with the interest expense x DSCR. When you do this you get a smaller debt level.
Step 1: Compute the Interest
Step 2: Compute the Interest x DSCR
Step 3: Compare the Interest x DSCR to the CFADS
Step 4: For periods where the limit from Step 3 creates a limit, reduce the debt service.
.
.
.
.
Results of this method are shown in the screenshot below where the deposits and withdrawls into and out of the screenshot are illustrated. In this case note that the IRR is a lot higher than method 2 where the debt size is reduced.
.
.
To illustrate this method I work through a step by step approach. The first step is to compute the deficit in the cash flow relative to the DSCR. You can compute the required CFADS at the target DSCR. If the cash flow is too low then you need to do something. The formulas are:
Required CFADS = Debt Service x Target DSCR
CFADS Difference = Required CFADS – Actual CFADS
If CFADS Difference is Positive — Money Available to Put in Reserve
If CFADS Difference is Negative — Money Must be Put in Reserve
You can then create a credit facility that looks for the point where the cash flow is needed. Once the credit facility is created you can look ahead until there is enough cash above the requirement to repay the debt.
Use an opening balance
Add: the negative requirement
Less: The accumulated when it is positive
Closing Balance
Creates a circular reference
Deficit CFADS = MAX(Required CFADS,
Method 4: Limit the Debt Service to the Interest Expense
In this method, the DSCR is increased in negative repayment periods to the interest expense. This method can cause a problem for bankers because to eliminate the negative repayment, the DSCR must be reduced. For example, if the CFADS is 100 and the DSCR is 2.0, the debt service is 50. If the interest expense is 75, the the repayment would be negative (25). In this case it would be possible to 1.33, below the target of 2.0 and then the repayment would be zero. As the repayment is more than results from the NPV formula, the tenor or the DSCR for the other periods could be adjusted. The formulas for implementing the method are shown below.
.
Results of the method depend on whether the amount of the debt is reduced. The screenshots below illustrate cases in which the debt size is fixed and the tenure is fixed. The IRR effects are illustrated on the graphs.
.
.
Method 5: Implement a Revolver Debt Facility
.
In this case a commitment is established and a working capial type facility is established. The commitment fee and the interest on the facility is included in the CFADS. The commitment is not drawn until the negative repayment occurs. In determing the repayment, the repayment must be adjusted to maintain the minimum DSCR. Equations to accomplish this method are demonstrated below.
.
Excel File with Analysis of Battery Replacement Causing Negative Repayment with Sculpting
.
.
Results for the case with the revolving debt facility are illustrated in the case below. Note the IRR in this case is closest to the case where the negative repayments are allowed.
.
.