This webpage demonstrates the difference in alternative terminal value methods including the growth rate method, the value driver method and use of a fade period. I hope to have finally make a model with alternative growth rates, returns and cost of capital that illustrates problems with alternative methods. I also demonstrate the importance of making normalization adjustments in the terminal period when using the growth rate method. My method of demonstrating problems with alternative terminal value methods uses a theoretical long-term model which demonstrates the true value with different growth rate patterns. The excel file with the alternative models is attached to the button below. The alternative models include the theoretical model, a growth rate model (with and without stable period adjustments); the value standard value driver model (named the black box model); the value driver model with a sudden and immediate change to the return in the terminal period; and a value driver model with a fade period.
.
.

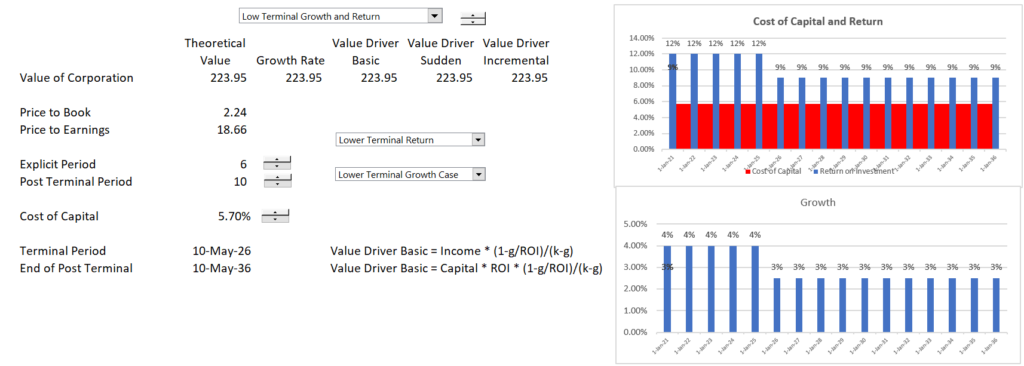
The screenshot below demonstrates how that when the growth rate changes over a fade period, only the incremental value driver method works. In this case the stable final method is applied to the growth method.
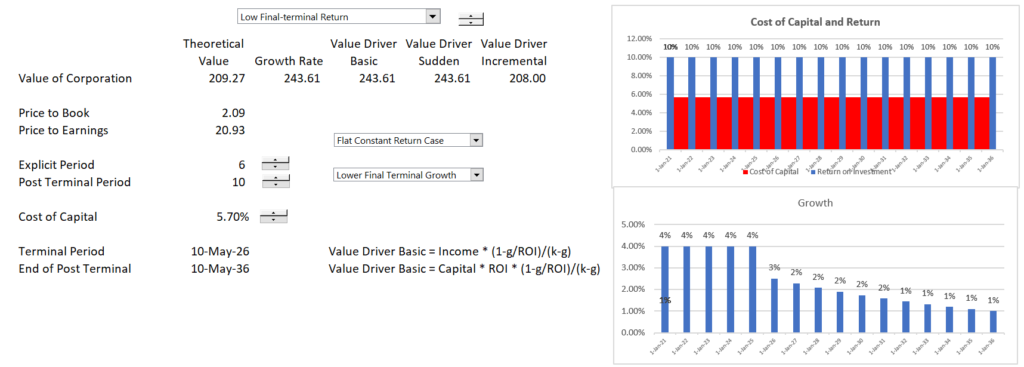
The screenshot below illustrates what happens when the rate of return changes over the fade period. In this case the growth rate method dramatically overstates the value. Note that the true value is 169 and the growth rate method results in a value of 370. The black box sudden method also overstates the value.
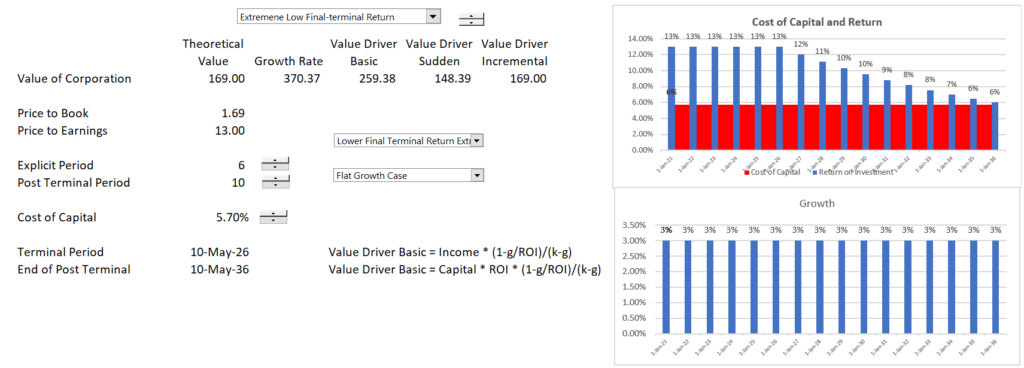
The screenshot below demonstrates the case with both changing returns and changing growth rates.
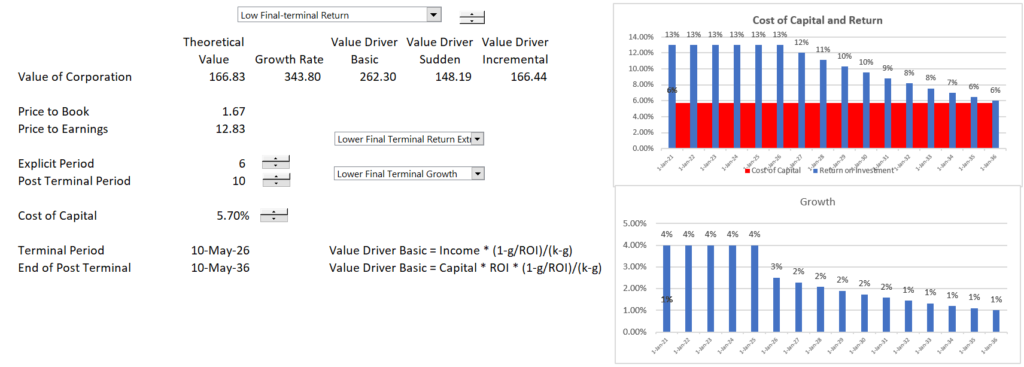
The case below demonstrates the case when the return is changing over the explicit period. This demonstrates that when the return is declining, the price to earnings ratio is low.
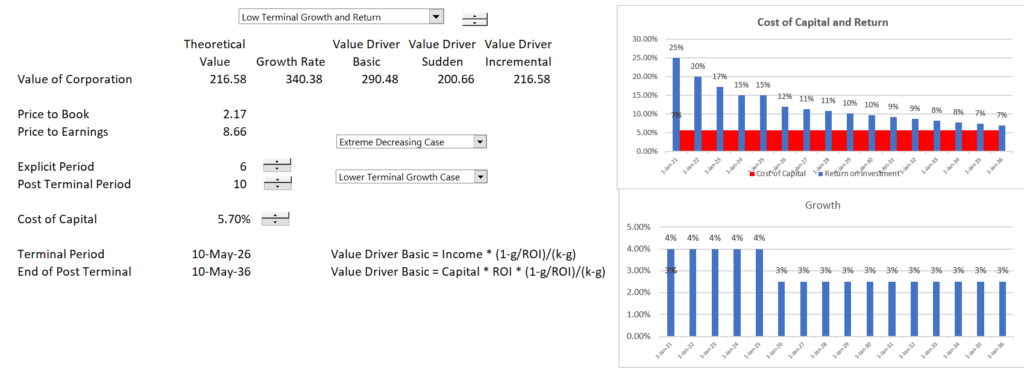
The case below illustrates the case when the return is increasing. In this case the P/E ratio is dramatically increased.

The case below demonstrates that if there is a sudden change and if the normalisation method is used, then all of the methods produce the correct result.