This article shows you how to prove that use of WACC or use of the un-levered cost of equity produces correct valuation of a corporation in the case where there is no tax shield on interest expense. Establishing a way to use cash flow components to prove valuation derived from classic WACC is essential for analysis of more complex valuation issues. The valuation proof is demonstrated by constructing a long-term model with growth where the debt to capital ratio is maintained at a constant level consistent with the assumption in the WACC or un-levered cost of equity as a firm grows. When the cash flow components are discounted at rates consistent with cost of capital in the WACC, the separate discounted cash flow of interest payments, new debt issues that fund growth, and residual equity flows have the same valuation as amounts in the capital structure. Working through this cash flow proof carefully is essential as a foundation for discussion for valuation of the tax shield provided by the interest expense. The tax shield case demonstrates that valuation can be established from using net of tax debt and the gross pre-tax interest rate in the capital structure.
Unfortunately, finance professors like Damoradan waste time with a bunch of meaningless formulas rather than developing proofs of different valuation concepts with cash flows. My good friend Karnen is admirable because he tries to follow along the various formulas, but I feel sorry for him. Instead, I have long believed that developing a careful excel model that may be quite simple (but not easy) is a much better way to think about and prove various various valuation concepts (even if the finance professors may not get credit when they write their articles.) Therefore, the proof of WACC without taxes in this case may at first blush seem obvious, but it is essential to work through.
The file that you can download by pressing the button below includes proofs of how applying cost of capital to different cash flows results in the correct valuation of cash flows in the case without taxes. In following through the example on this page you should use the assumption that the tax rate is zero. It is not as easy as you may think to illustrate basic rules of WACC, DCF and value when a company is growing. In particular, the growth in enterprise value must include a debt funding assumption and that net funding must be included in cash flow. But we must start with a basis for proving ideas. We must have a way to prove true value from the present value of cash flow components. Once we prove true value, you can test different tax shield formulas.
Excel File that Demonstrates Valuation from WACC or Ku Produces Corrcect Cash Flow Without Tax
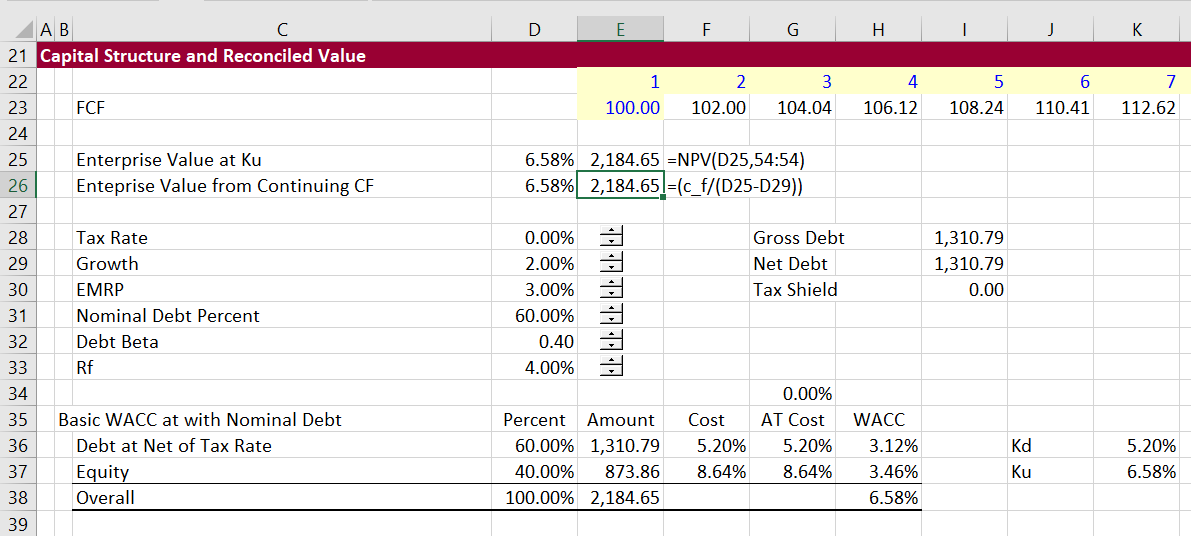
The first screenshot below introduces the valuation proof. In this case the WACC or the Ku is established from the un-levered beta. Without tax, the WACC and the Ku are the same. In the example, Free cash flow is 100 and grows at 2%. This leads to an enterprise value of 2,184 as shown in rows 25 and 26 of the screenshot below. The value can be computed as the cash flow divided by (WACC-g). It can also be computed as the net present value of the cash flow row that continues for 700 years. The assumed debt is 60% and the assumed equity is 40%. With the debt cost of 5%, the implied cost of equity is (WACC – Debt Cost x Debt to Capital)/Equity to Capital. As shown in the capital structure analysis, the resulting cost of equity is 8.64%. When the enterprise value is separated into debt and equity, the resulting debt is 1,311 and the resulting equity is 874. The next screenshots demonstrate how you can compute cash flow components starting from the 100 free cash flow and confirm the valuation.
The next screenshot demonstrates how the cash flow components reconcile to the value of different items from the capital structure. The first line shows free cash flow and then the line titled “value of company at all equity cost of capital” shows the progression of enterprise value into the future as the company grows. Below the value that is derived from the free cash flow, the debt is computed. As the debt is assumed to be at market value and the debt to capital is assumed to be constant, the market value of debt is 60% of the enterprise value. Once the debt is established, the interest expense can be computed. The present value of debt at the cost of debt capital for debt investors accrues to debt holders. This should be clear so far.
In addition, the change in the net value of the debt that occurs as a company grows is a source of cash flow (an addition to free cash flow). With more debt, there is an increase in cash flow from the perspective of the cash flow to equity as the debt produces cash. After the interest expense and the new debt is computed, the cash flow to equity can be established (line 65). The value of the interest (2,130) and the new debt (819) should be discounted at the interest rate (5%). The value of equity can be computed as the equity cash flow using the cost of equity capital (8.643%). The value of the debt and the value of the equity are shown in separate lines. Importantly, the value of equity as well as the value of interest less the value of the cash flow from new debt are the same as the values in the capital structure. This is demonstrated in the next screenshot.

The screenshot below shows that the cash flow components reconcile to the capital structure. Begin with the left column. This column simply shows the enterprise value, the debt and the equity from the capital structure. The middle column shows the value of interest and the value new debt financing that are measured using the interest rate. The equity value of 873.86 is the present value of the equity cash flows at the equity cost of capital of 8.64%. The bottom reconciliation in the middle column shows that when you subtract the value of interest and the value of new debt from the enterprise value you get the same value. The right hand column shows the components of debt valued from cash flow and the equity value is the cash flow valued at the cost of equity.

You may be saying that this whole exercise is a little simple and basic. First, it took a while to establish that with growth, the increase in market value of debt must be included as a cash flow. This cash flow is the next year debt amount less the current debt amount. Second, the exercise of verifying value in the WACC calculations is used to prove the correct method of measuring value of the tax shield in the next webpage. You have to have an opinion as to the discount rate used to value the tax shield and demonstrate that your method is consistent with valuation of detailed cash flow.
Video Explanation of Cash Flow Reconciliation