On this page I include my analysis of how to reconcile LCOE calculations with Lazard. In working through the calculations I emphasize the importance of computing the real and not the nominal LCOE when comparing different technologies and I also discuss the importance of not overstating the cost of capital (I know everybody and especially private equity wants a high return, but this creates big distortions inthe measurement of the cost of capital). I demonstrate that you can compute the LCOE with a series of calculations using the PV and PMT formulas (not the NPV). The file attached to the button below allows you to input characteristics of a project and develop the LCOE both consistent with the Lazard calculation and improved for properly incorporating inflation, cost of capital and taxes.
The file attached to the button below matches a project finance model and equations that use the PMT and PV functions to compute the levelised cost of electricity. The file attached to the button below includes a data set with the Lazard operating assumptions and many different financial inputs. The file demonstrates the importance of project finance in evaluating the cost structure of capital intensive investments.
.
.
The impact of different cost of capital assumptions are shown on the diagram below. You can select different technologies and illustrate the effect of the economic assumptions. The first screenshot taken from the file shows the dramatic effects of different assumptions on a nuclear plant where the LCOE can be measured as much as USD 173 per MWH down to USD 54/MWH. I insist that the LCOE of USD %$/MWH is correct.
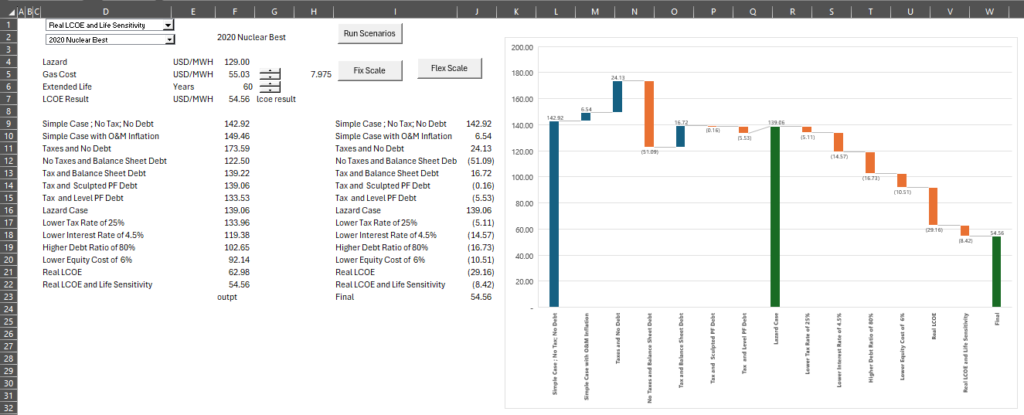
.
A similar graph for a natural gas combined cycle plant is shown below. In this case there is a much less dramatic effect of the assumptions because so much of the overall cost is the cost of fuel. In this case I assumed a European cost of gas.
.

.
Using the LCOE Model Attached to the Button Above
.
If you just want to use the LCOE model, go to the first page and enter your operating inputs for the cost of the plant, the O&M cost etc. This is shown in the screenshot below. You will see the nominal and the real cost in column D. Again, I insist that the real cost of USD 33.21/MWH shown on the page is the correct number. You can use the drop down box to LCOE for different technologies. I have included operating data along with the LCOE reported by Lazard to demonstrate that you can get the same approximate number. If you want to reconcile with Lazard, use the second drop down box around cell E3.

.
Once you have the technology assumptions, you can compute the economic variables including inflation rates, cost of capital and tax rates. The inputs for the financial assumptions are shown in the screenshot below. You probably do not agree with my low cost of equity assumption but this and a reasonable interest rate are essential drivers to the LCOE. You can of course put in your own assumptions. At the bottom of the page I have put in the depreciation assumptions.
.

.
Reconciliation with Project Finance Model
The file contains a project finance model where the LCOE is input for the price (on a real or nominal basis). You can then press the goal seek button on the first page and assure that the project IRR and equity IRR that are input in the financial assumptions produce the correct result. Using the example with the nominal LCOE of 46.71 and the real LCOE of 33.21, you can navigate to the project finance model page and see that the LCOE produces the correct IRRs. The screenshot below shows how the real LCOE of 33.21/MWH is inflated in the model.
.
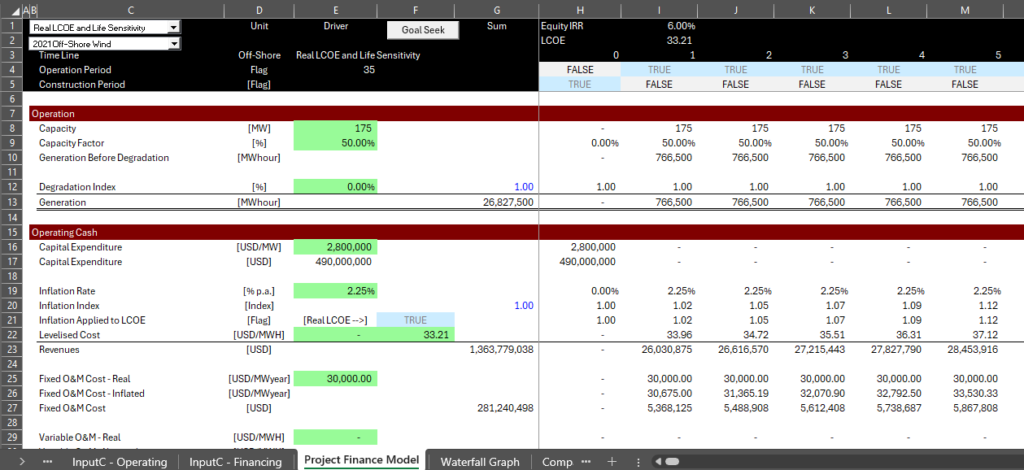
.
The bottom part of the model shows that the price produces the input nominal and real returns and in particular the equity return. A major idea of this analysis and spreadsheet is that you do not have to make a financial model and then press the goal seek button. You can see on the spreadsheet below that the NPV of the equity cash flows at the target Equity IRR is zero. This proves that the calculation of LCOE using the PMT and PV formulas work.
.
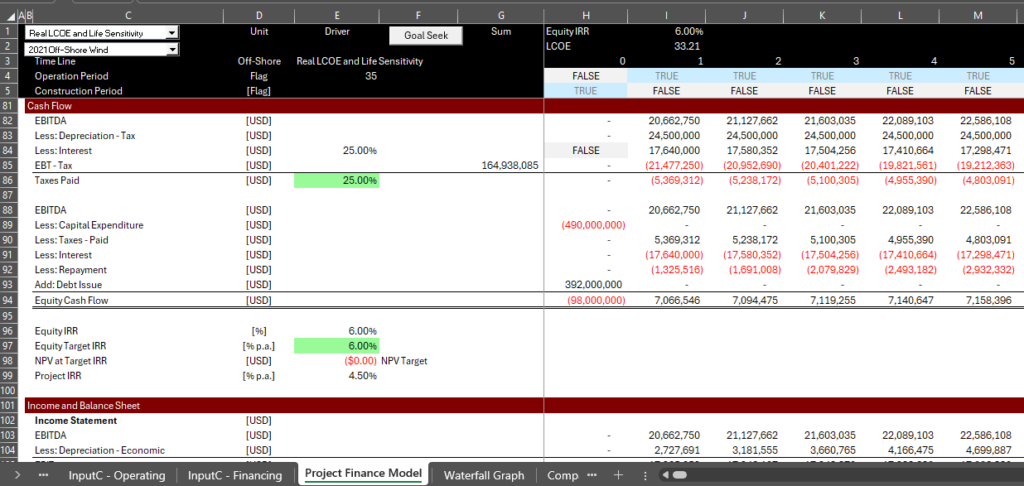
.
Using PMT and PV formulas to Compute LCOE and Produce the Target IRR
Calculations of the LCOE using PMT and PV formulas are shown on the first page after the assumptions. The idea of this page is to show you produce the same result as with the goal seek and financial model. Without taxes, inflation and degradation the formulas are very easy. Complications from these factors are not that bad once you practice a few times. The good news is that you then have a tool to compute the LCOE of all sorts of things. The screenshot below illustrates compuations using PMT and PV. Videos at the bottom of this page describe some of the features of the model and some general financial modelling principles.
.
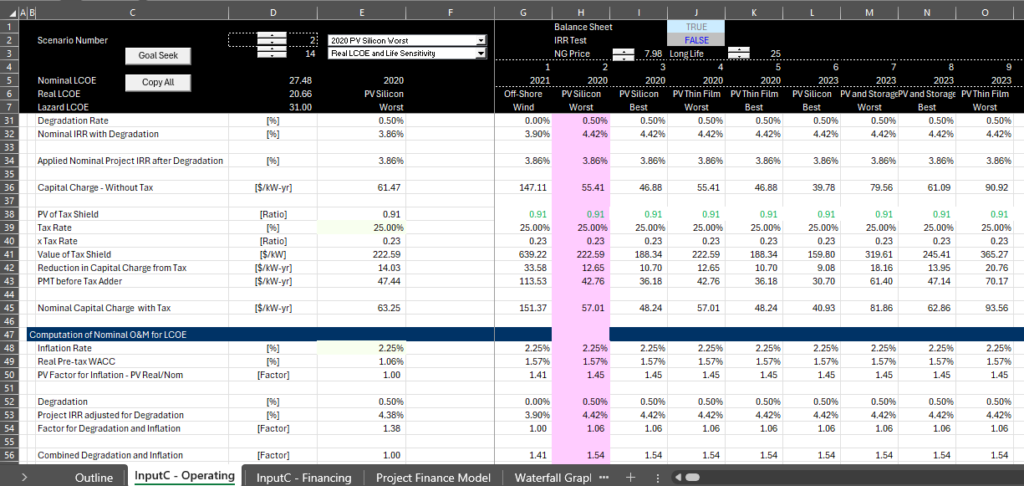
.
General Comments About Lazard Reports
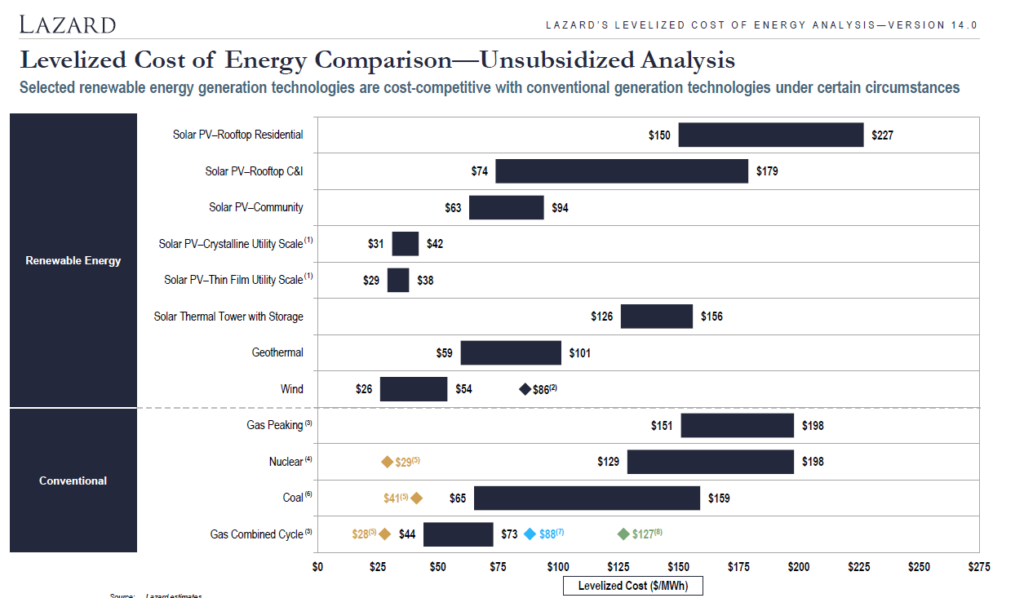
For years now the inestment bank Lazard has published statistics on the levelized cost of electricity. They publish the costs of alternative technologies in a football field diagram. Lazard seems to spend more time on the presentation of graphs and less on the key assumptions that drive the analysis. In terms of the calculations, Lazard does not convert the data into real terms which is essential for economic analysis where projects with different mixes of operating and capital cost are compared (if inflation adjustments are not made, the LCOE favours projects with more operating cost). An example of a football field diagram is shown below.
.
.
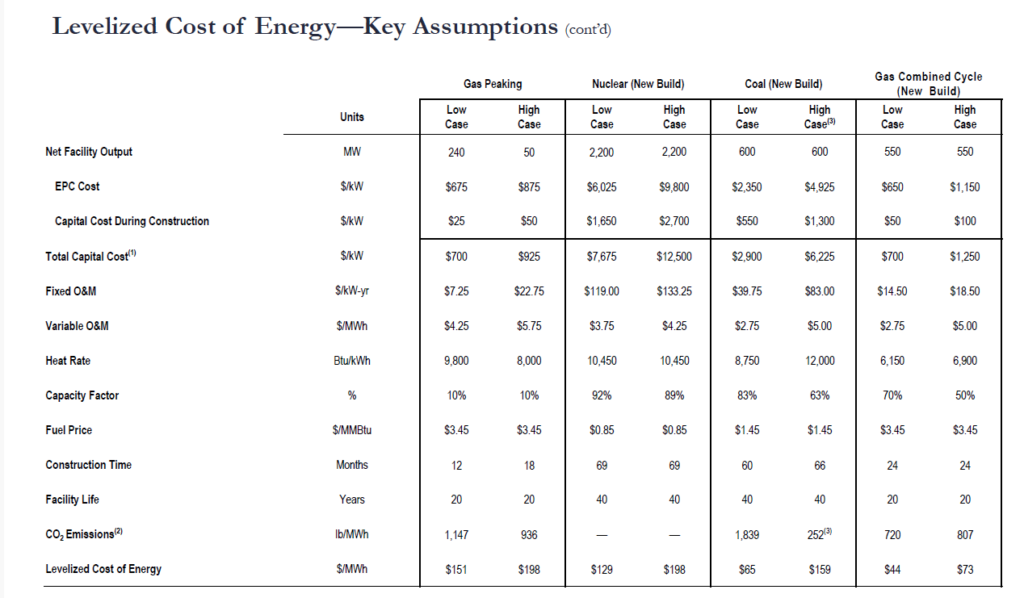
I have reconciled the 129 per MWH in the above graph. This can be done with a formula that takes a couple of steps. The first thing you can do is to go down to the bottom of the Lazard report and find the key drivers of the cost including the capital cost per kW, the operating cost per kW year, the fuel cost and the operating life. The manner in which Lazard presents this data is shown below.
.
Videos of LCOE
.
The first video below presents and overview of LCOE issues in the context of project finance. The picture os of my friend John Boudreau with whom I used to discuss all sorts of issues related to electricity. He was really brilliant and we drank a lot of beer when discussing the issues. Unfortunately John is no longer here and I miss him.
.
.
.