This article explains how to resolve one of the most debated issues in corporate finance; that is how to value interest tax shields when constructing a discounted cash flow analysis. There are numerous articles with long formulas and alternative methods such as APV that have addressed the issue for decades. But the articles and valuation methods miss the fact that the value of interest tax shield in valuation boils down to a simple idea. Even though the everybody uses the market value of debt rather than the book value, this idea does not extend to the interest tax shield. When the fundamental notion of the market value of debt as the present value of fixed obligations incurred by the firm is recognized, the economic and financial resolution becomes clear. The capital structure must incorporate the net of tax rather than debt that is not adjusted for the tax shield. This use of net debt can be proven with valuation of separate cash flow components that was introduced on the prior webpage. The same method of separately valuing cash flows demonstrates that other methods do not produce a correct value.
McKinsey, Damoradan and other finance professors continue to confuse the issue. They are wedded to measuring each piece of the capital structure at its nominal outstanding value (rather than the market value of future obligations) and then attaching net of tax cost of capital to the different items. They cannot get out of the hole of recognizing that if you understand that the market value of debt should be used, from the standpoint of the firm it is the value of future net of tax fixed obligations. It is not the nominal value of debt that is issued by the corporation or the value from the standpoint of investors who do not receive the tax shield benefits.
Theory of Treating Debt at the Net of Tax Value of Future Obligations
In valuation and finance texts including texts by Damarodan and the McKinsey Valuation book, various methods are typically described. Some of the most irritating discussion is in a HBS article that seems to promote the APV method as some sort of advanced method that better reflects management strategy. An example of discussion of different methods that say nothing about any underlying theory of how tax shields should be value is illustrated below.

After introducing valuation methods with different fancy titles things typically become even more irritating. You get all sorts of formulas that are just different versions of a WACC table that shows the percent of debt and equity. As shown below, the these formulas can start with computing the unlevered beta. But it is simply unforgivable that the beta on debt is so often assumed to be zero. Note that the Bu does not properly account for the reduction in economic leverage caused by the reduction in fixed obligations. Why these fancy professors and consultants cannot figure this out is stupifing.

A much better way to think about the effect of a tax shield on interest is to think about a house with and without the shield as shown below. This diagram illustrates the equity value you would have in a house with and without a tax shield. The starting point is the value of the house which is 100,000 whether the tax shield exists or not. On the left hand side, there is no tax shield. In this case, the nominal amount of the debt at an interest rate of 10% yields a value of equity 40,000 because of the debt that has a value to both investors and to you of 60,000. To make the case simple, the loan is assumed to be a perpetual loan where the value of the loan is the nominal interest payment divided by the interest rate.
On the right hand side of the diagram, the loan is assumed to have a tax shield from a tax rate of 40%. This means that even thought the nominal loan balance is 60,000, because the interest payment is lower (subsidized), the effective leverage to you should be computed from the lower interest payment. Note that the reduced interest below the market could come from some kind of gift from God or other subsidy. But the market cost of capital or interest rate on debt remains at 10%. This is because the entity giving you the loan faces the same economy-wide interest rates and risks. Therefore, the value of the fixed obligation at market value should still be discounted at a rate of 10%. In terms of valuation, assume the beneficial tax shield can be assumed by a new buyer. Then, when you sell the house, your equity value is increased by the subsidy on interest payments. The equity value increases from 40,000 to 64,000 because of the lower value of debt. In addition, the effective leverage has declined. If the value of the house — 100,000 — declines or increases, the impact on the equity value is less with the subsidized interest rate. In the extreme case if the interest rate is zero and the leverage is zero, the change in value is not levered at all.

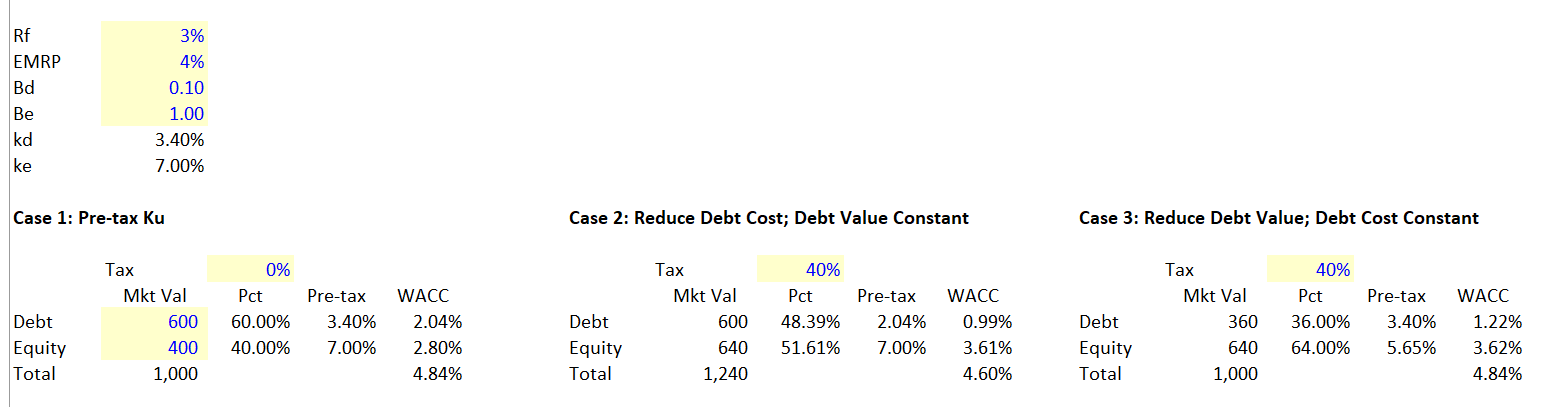
The screenshot below illustrates the change in value from a tax change on the capital structure and value using different assumptions in which enterprise value is used instead of the value of a house. In the first column, the capital structure and value is shown in a no tax case. Here the value is confirmed from a detailed cash flow analysis (as demonstrated the prior webpage) with a debt value of 600 and an equity value of 400. In the second column a traditional WACC capital structure is used after a tax change that creates a tax shield on interest. The fundamental free cash flow is assumed not to change (perhaps all of the tax change is allocated to consumers in price increases). It is likely the observed equity beta has not changed and the estimated cost of equity would be similar (it should not be as the leverage has changed). The value of the tax shield is 40% x 600 or 240. This value accrues to equity. The problem with WACC method in the middle column is that if the nominal amount of debt is used (as it typically is), the enterprise value is over-stated. In addition the WACC is distorted because the percentages are applied to the nominal debt and not the market value of debt to the firm.
The third column illustrates a much more sensible valuation and cost of capital analysis. Here the debt is reduced to reflect the lower fixed obligations to the firm. The effective market value of debt is reduced from the perspective of the firm by (1-tax rate). In this case the Ku is assumed to be the same (although in computing the leverage in a sample, the leverage should be changed). When the leverage is changed to reflect the reduced fixed obligations and the equity is increased to incorporate the value of the tax shield. Here the Ku and the enterprise value from the free cash flow do not change consistent with the fundamental assumption. The gift that the government or God or somebody else gives you in terms of the interest rate you pay relative to the market cost of debt is transferred from fixed cash flows for debt outflow into equity cash flow. The value of the tax shield is a transfer among the funding providers and it does not in itself change the free cash flow or the enterprise value.
Proof of Using Net Debt to Capital with Cash Flow Model
In the prior page, a model was introduced without taxes and a tax shield. This demonstrated that in a case without a tax shield, the WACC method or the Ku cost of capital produces a correct allocation of value between debt and equity. Here, the model is adjusted for taxes. The cash flow model with discounting different cash flow at the market cost of capital proves the method of using the net of tax debt in the capital structure is appropriate and that any method which uses gross debt does not produce correct results. The file that contains the proof of the using net debt in the capital structure is in the file that can be downloaded below.
The screenshot below illustrates how using the net debt results in the correct cash flow. In this case a nominal amount of debt of 60% is assumed. After multiplying by (1-30%) or one minus the tax rate, the net debt in the capital structure is 42% rather than 60%. The Ku is assumed to be the same as in the no tax case, resulting in a lower cost of equity. Using the EV which is still the net present value of free cash flow, the debt is 917.55 and the equity is 1267.10. When you look below the capital structure, the same values are produced by working through the cash flow payments, the cash flow from the interest tax shield and the cash flow provided by the increase in new market or economic value of debt. In the middle column, the NPV of the interest at the market or pre-tax interest rate is computed as is the interest tax shield. When valuing the gift from the government or somebody else, the discount rate is still the market debt rate for investors. Maybe the trickiest part of the proof is understanding that the value of debt that appears on an economic balance sheet is the net of tax debt. The increase in fixed obligations provides equity cash flow.
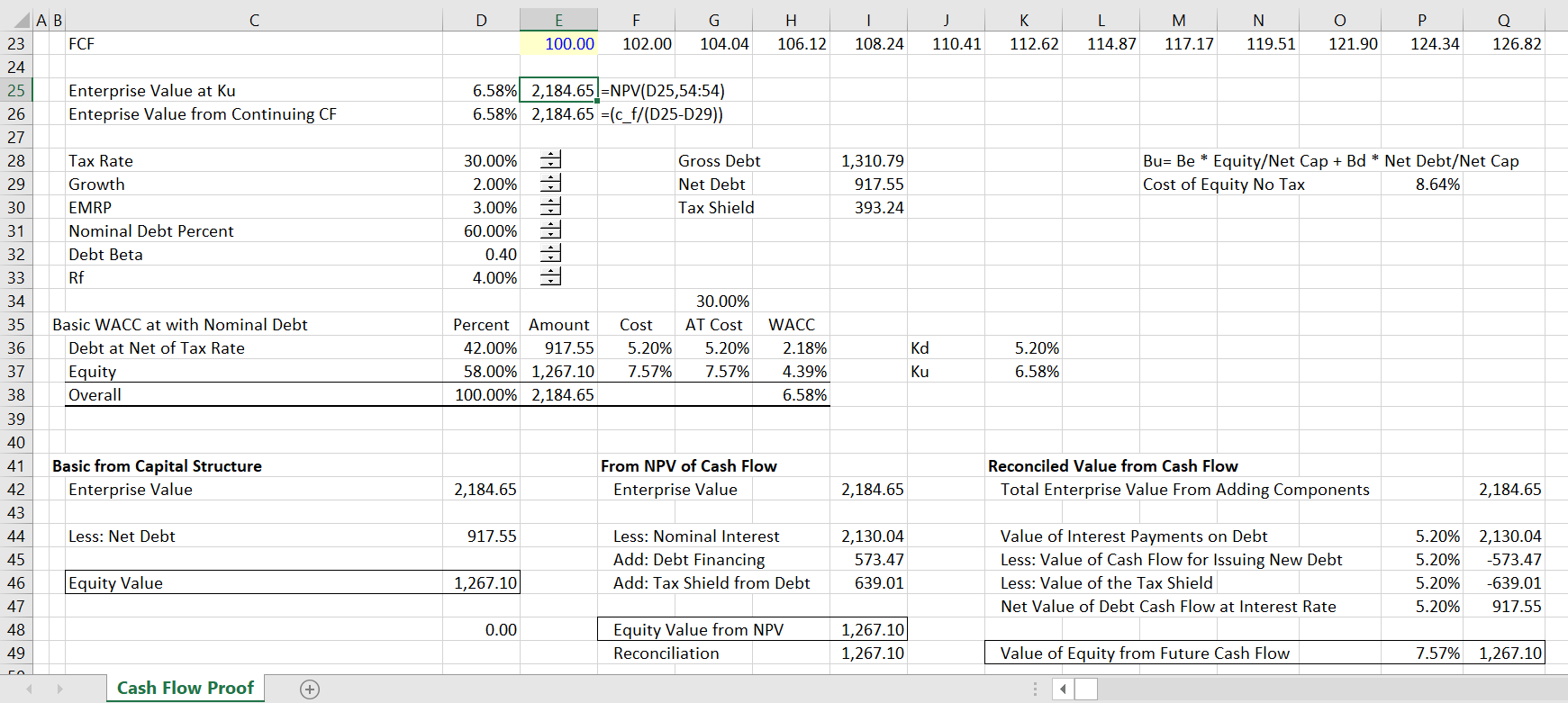
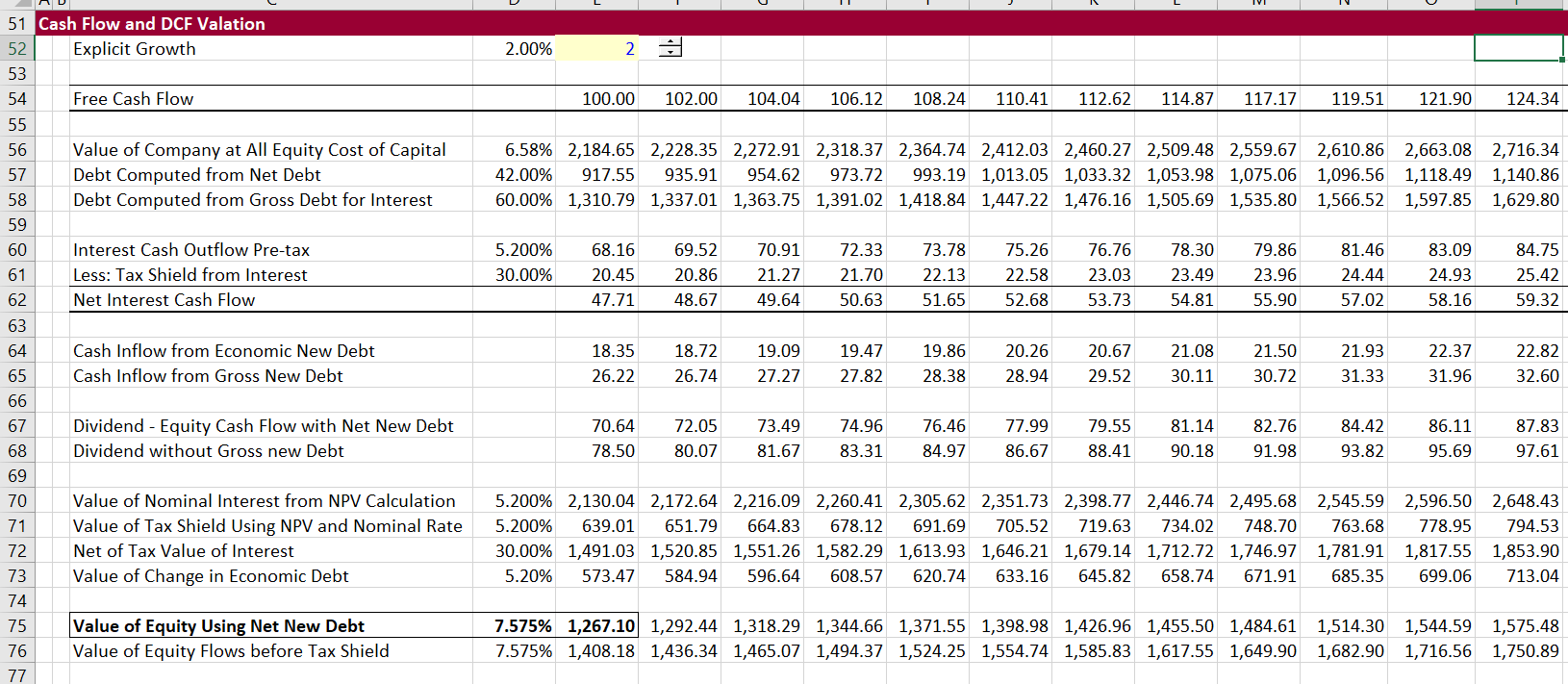
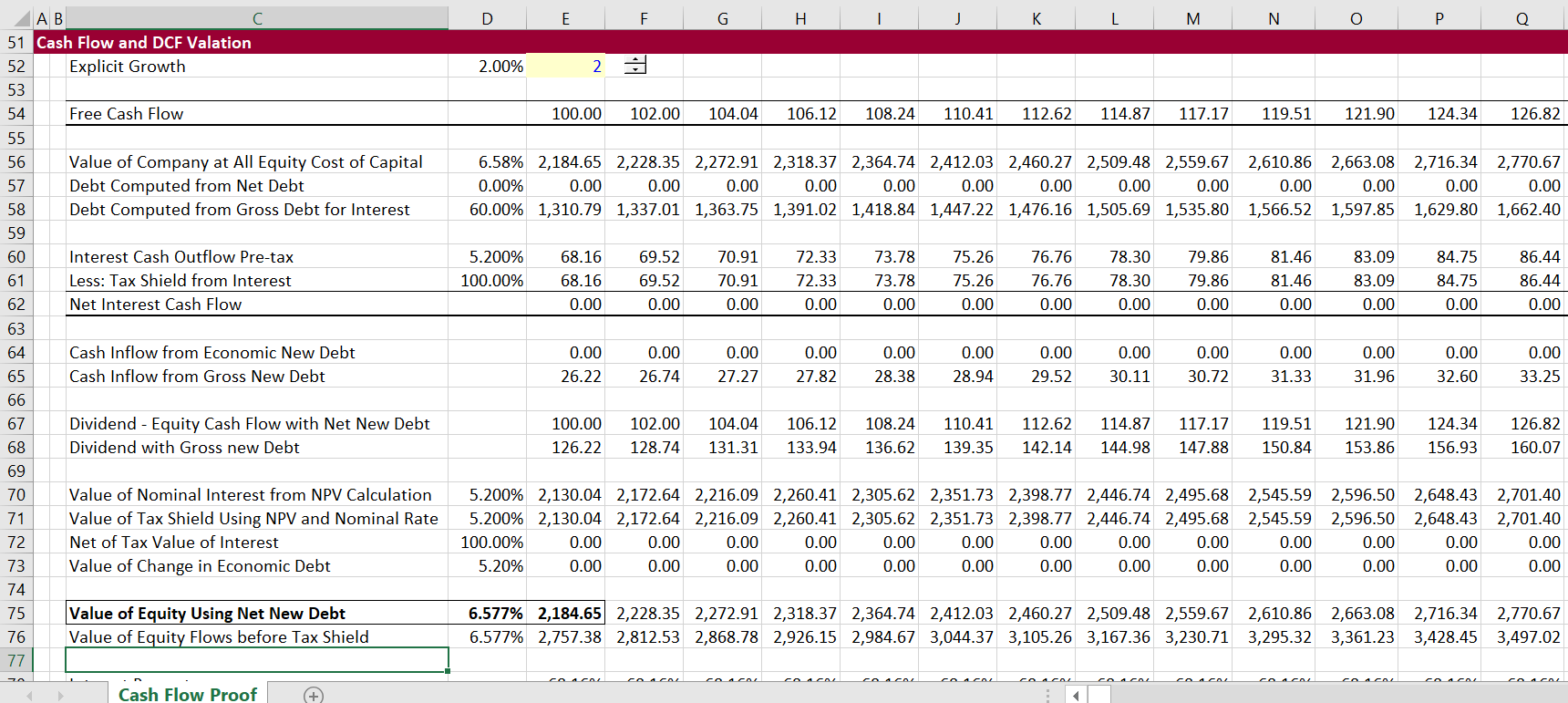
The most difficult part of the proof is how to value parts of the debt flows. The enterprise value (after tax) is not a function of the financing and the associated tax effects. This assumption of free cash flow being independent of tax shield and financing has been consistent throughout this discussion. It is necessary to understand the simple model without tax to understand the value of the tax effects of cash flow. As the enterprise value progresses and increases with growth, so does the amount of the debt, both nominal and market value. While the nominal interest is an outflow of cash derived from the gross nominal amount of debt, the new debt is an inflow of cash. This is shown in lines 56 to 62 in the screenshot below. In the cash flow layout below (remember this cash flow is approximately forever — 700 years — growing at 2%).
The enterprise value grows over time and so does the debt. The gross debt and the net of tax debt is computed as a percent of the enterprise value in lines 57 and 58. The gross interest and the tax shield is computed from the gross debt value. The interest flows and the tax shield cash flows can then be discounted at the market interest rate that has nothing to do with the gift given to the firm. The interest rate for discounting should not be adjusted for taxes as it is the cost of capital to capital suppliers. The cash inflow from new debt is the most difficult part to understand. Specifically whether the debt should be measured at its economic or market value to the firm or whether the debt should be measured at the gross amount of debt that provides cash flow. The answer is that the market value should be used. To illustrate why this is the case, I have made an extreme case where the interest tax shield results in zero interest payments.
Continued Discussion with Extreme Case of Tax Shield Equal to Interest Cost
To demonstrate why the proof above is valid, you can consider an extreme case where the tax shield on interest is equal to the amount of the interest (perhaps the government gives a very big tax break for interest and has lower tax rates on other things). With this assumption there is no net payment for debt. Here, all of the cash flow accrues to equity and the equity value is equal to the enterprise value as demonstrated in the screenshot below. In the screenshot below, the market value of debt is zero because the tax rate used to produce the tax shield is 100%. The equity value is equal to the enterprise value as a result. You may be thinking that the equity value should be higher than the enterprise value because of the cost free capital gift that has been given to equity holders. But remember rule number one about valuation — it is the future cash flow value that is being measured and this value does not depend on historic fund raising. The total equity value and enterprise value depends only on the cost of equity capital and the equity cash flow. In this case the equity cash flows are identical to the free cash flows and the equity cost of capital is identical to the all-equity cost of capital (or maybe WACC). The example is basic: total enterprise value comes from free cash flow. This free cash flow can be only allocated to debt and equity. If there are no debt obligations to pay, all of the value accrues to equity holders.
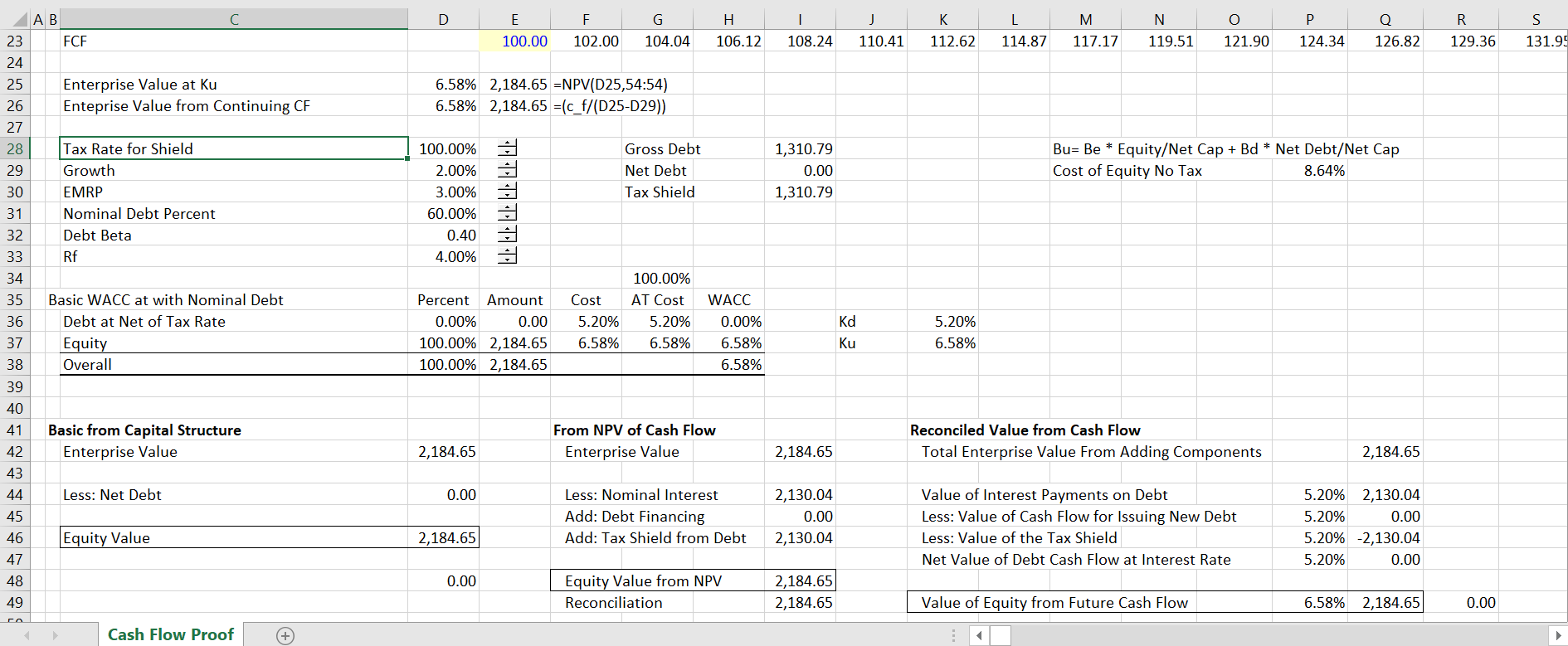
The screenshot below demonstrates the valuation of separate cash flows in the extreme case where the tax shield results in no outflows for interest net of the tax shield. In this case, the economic value of debt is always zero. When the firm grows, new debt is raised. But there is no fixed obligation associated with the new debt. If the gross debt were put on the balance sheet, the balance sheet would not have a constant capital structure. The new debt would distort the balance sheet. Instead, by using the economic value of the debt, the new nominal debt is implicitly transferred to equity as the firm grows. This new debt should be valued at its economic obligation of zero and the nominal amount of debt should not be included in cash flow. Consider the second year. The cash flow and the value increase. There is corresponding more new debt which shows up as positive cash flow to equity. This cash flow is transferred to equity as soon as it is issued.
Consider the case where a firm is completely stupid and issues new debt at above the market value as it grows. Even though the company may raise debt of 17.5, its equity value has gone down by 35. The decline in value from growing and stupidly paying too much for debt each time you grow. In the opposite example, each time you grow, you would put debt on the balance sheet and thereby increase equity. This debt disappears because of tax shield. As such, the change in the economic value of the debt must be used in the cash flow proof.
Summary
1. Tax Shields from Interest Deductibility in WACC Can Be Resolved with Gross and Net Capital Structures. The excessive discussion about how to value tax shields associated with debt is a colossal waste of time.
When you recognize that the tax shield is equivalent to a reduction in the coupon rate on debt, the proof of how to treat the tax shield becomes clear. The market value of debt to the corporation is reduced to when the coupon rate falls and the equity value increases. For example if debt was 1,000 at with an interest rate of 10% and the coupon rate is reduced to 6%, the market value of debt decreases form 1,000 to 600. If the opportunity cost of debt for providers of funds is 10% both before and after the coupon rate decrease, the value of the debt declines to 60 of interest/10% or 600.
This example is just the same as the tax effects of the interest shield at a 40% tax rate. Using the simple an basic principles that the fixed cost to the corporation is reduced from the tax shield and that the opportunity cost to providers of debt does not change from the corporate tax rate, the following equations quantify the tax shield. The second method is equivalent to the traditional WACC implementation.
Tax Shield Percent = Gross Observed Market Debt to Capital * t
Net Equity Percent = Gross Equity Observed/(1-Tax Shield Percent)
Net Debt Percent = 1- Net Debt Percent
Ku = Kd * Net Debt Percent + Ke * Net Equity Percent
Ke = [Ku – Kd * Net Debt Percent]/Net Equity Percent
Bu = Bd * Net Debt Percent + Be * Net Equity Percent
Be = [Bu – Bd * Net Debt Percent]/Net Equity Percent
4. Circularity in WACC and Valuation from Tax Shield can Easily be Avoided. As the equity to capital ratio is computed using the market value of equity and, in turn, the market value of equity requires a value of WACC that is in turn driven in part by the equity to capital ratio. This implies a circular reference seems to exist. This is not much of a problem when the Bu and Ku is established from a comparison set of companies. The remaining circular reference from re-levering the beta can be easily resolved.
5. Target versus Actual Capital Structure Does Not Matter With No Interest Tax Shield. If there is no tax shield, the WACC should not change if you use different capital structure assumptions because the cost of equity changes to compensate for risk created by gearing. This means that without taxes, use of a target capital structure in the context of DCF is not beneficial, necessary or relevant in terms of accuracy or theory. Without the interest tax shield, when the cost of equity is derived from re-levering the unlevered beta using the market value of debt at the valuation date, the result is exactly the same as if the company moves to a target capital structure.
6. APV does not add anything new to valuation. Correct application of the WACC accounts for all items in the bridge between equity value and enterprise value in the WACC calculation. Investment bankers typically do this with using net debt rather than gross debt in computing WACC. Similar adjustments to the WACC should be made for associated investments not included in EBITDA, the fair value of derivatives, discounted operations and any other items.