On this page I address the issue of inflation when computing levelised cost or the total cost of operation. When computing the levelised cost of electricity or the levelised unit cost of something else like the oil price necessary to break even on an investment, the ultimate objective is make some kind of economic analysis which compares different strategies and/or technologies. When making an analysis, inflation can distort the analysis when not computed correctly. In this page I show how to compute the real levelised cost or the levelised cost adjusted for inflation. This means that a flat unit cost in nominal terms is not computed, but the cost is in real terms where the levelised cost increases over time with inflation. This real cost can be compared to things like the cost of your electricity bill per kWh or the cost of natural gas. If you use the nominal LCOE that is in a sense the price at the middle of the life of a solar or other project, you would have to compare your electric bill in 10 or 15 years to the LCOE of the solar project. To compute the real LCOE, I show some techniques that use the PMT function with the real cost of capital rather than the nominal cost of capital. As with other issues, I have included a file with the examples and methods discussed on this page. The LCOE calculator attached to the button below includes inflation adjustments and analysis of the real LCOE.
.
.
.
Formulas for Computing Carrying Charge for Real versus Nominal Levelised Cost
.
When computing the levelised cost of electricity or the levelised unit cost of something else like the oil price necessary to break even on an investment, you can compute the current price necessary to meet the required return. If you compute the real return and then the real carrying charge, the inflated real carrying charge will produce the target nominal return after it is inflated.
Real Return = (1+Nominal Return)/(1+Inflation Rate) -1
Real Carrying Charge = PMT(Real Return, Life, Capital Cost)
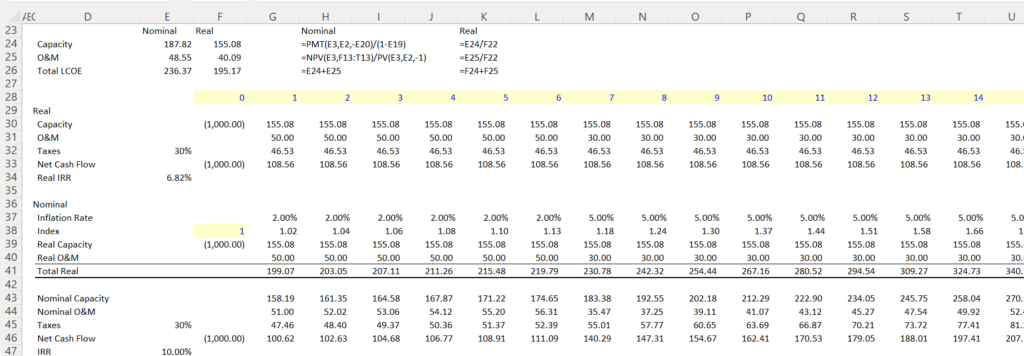
The screenshot below works through how to compute the real levelised cost. When you think about things, the levelised nominal cost is a silly number. Think about a hydro plant than may last 80 years. The nominal levelised cost is the flat value over 80 (with a minor adjustment for inflation in O&M expenses discussed below). With even a minor rate of inflation like 2%, the real value in 80 years is a very small percent of the value in the first year (divide by 1.02^80) — 4.9 times. It would be much better to compute the current value that, when inflated, gives you the target return. In simple terms this involves using a real cost of capital as described below.
To begin the discussion, the screenshot below demonstrates how I have input an inflation rate and also computed a required real return. The required real return is computed as:
You can then use the real return instead of the nominal return in the carrying charge calculation with the PMT function. You can also then compute the total carrying charges and the LCOE with the inflation rate.
.
Adjusting the Operating Expense for Inflation when Computing Nominal Levelised Cost
.
Note in the above screenshot that the O&M cost is different for the real LCOE than for the nominal scenario. This is because the O&M cost should increase with inflation. After you levelize the O&M cost, it should be higher in the nominal case where it is (inappropriately) held flat. To compute the equivalent levelised O&M cost, you can apply the formula:
Inflated O&M Factor = PV(Real Rate, Life, -1)/PV(Nominal Rate, Life,-1)
When doing this, you will want the real IRR on the top and the nominal on the bottom to make sure the factor is above one. Apply this in the LCOE formula and not in the financial model. Note that this is not the NPV formula; it is a formula that allows you to input a payment (-1) and produces the present value, The PV using the real rate is higher than the nominal rate. So, the value of this factor is above 1. I you would do this for a single year — for example (1+real rate)^10/(1+nominal rate)^10 — this results in the inflation rate. So the formula over time is like computing this increase in inflated cost over time.
As with the first case, I have made a little financial model that proves the approach. I compute a little model for both the nominal case where the absurd assumption is made that the price never changes. But this time I allow the O&M cost to increase with inflation. With the price computed using the increased O&M, the financial model produces the correct IRR that is input as the target IRR.
.
Financial Model Verification Using Real LCOE
.
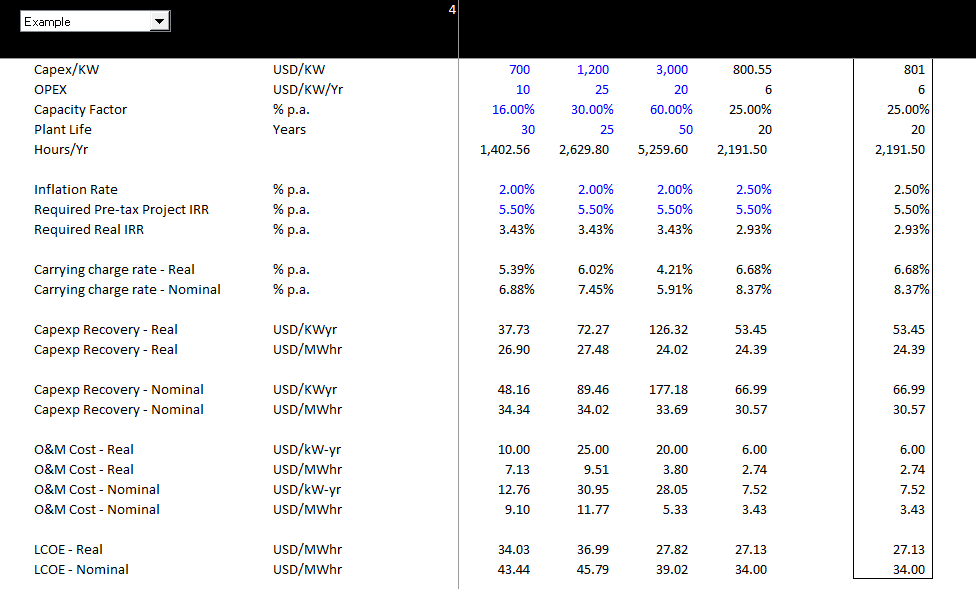
In the screenshot with the simple model, I also show how the model in the real case. In this case (the bottom part of the screenshot), the computed real LCOE is increased by the inflation rate as shown in the price line (27.8 followed by 28.50, followed by 29.21 etc.). The O&M is inflated in both case starting with the real level (this is the value of 6/kW-year multiplied by 1,000 to put the values in terms of MW.) With these values, both the real value and the nominal value produce the target return of 5.5% that is input as the target in the above screenshot.

.
Computing Real and Nominal Levelised Cost or Total Cost of Operation when the Inflation Rate Changes
,
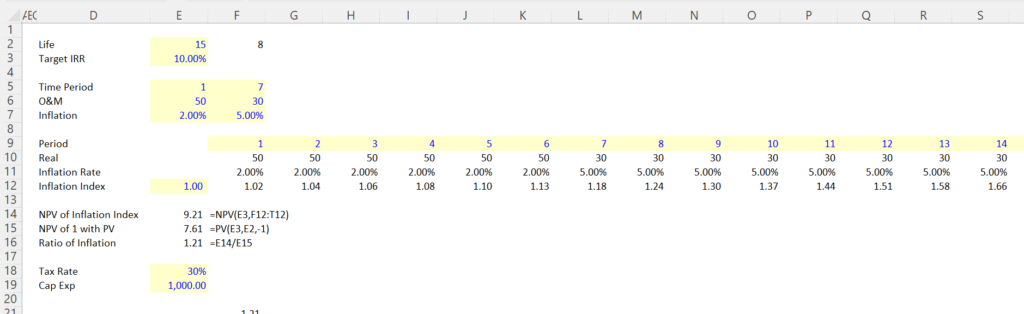
I have tried to come up with a simple way to adjust the levelised cost when the inflation rate changes. Unfortunately for these calcualtions you will probably have to compute an inflation index and then make compute the ratio of the nominal PV to the real PV as described below.
Step 1: Compute the NPV of the inflation Index using the nominal pre-tax target IRR (the pre-tax discount rate without a tax adjustment).
Step 2: Compute the PV of 1 over the entire period using the PV formula
Step 3: Divide the PV of the Inflation Index by the PV of 1 to Establish the inflation ratio.
Step 4: Compute the capacity payments and the operation payments using nominal data and the nominal discount rate.
Step 5: Divide the levelised nominal capacity payments and the level nominal O&M payments by the inflation factors to establish the real levelised cost
.
Illustration of Changing Rates
Steps 1-3 are illustrated in the screenshot below. Note that you use a simple NPV formula with the inflation index and the PV formula for denominator.
The computations of nominal and real LCOE are illustrated below. The capacity payment can be computed with the PMT formula, but the O&M must be computed with a PV formula.
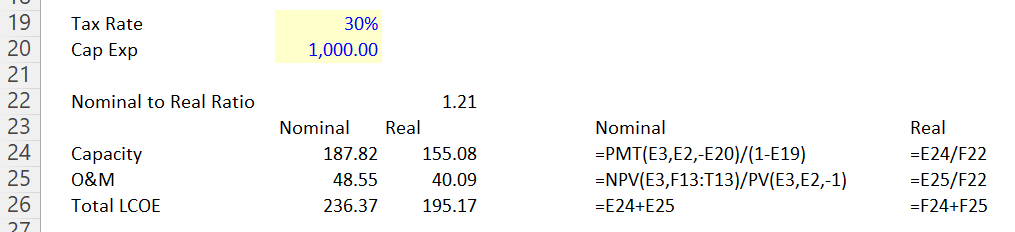
Proof of the use of real and nominal. Note how the real numbers are inflated to come up with the nominal values. After taxes the IRR target of 10% is met.